练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．某企业2003年的生产利润为5万元，采用一项新技术，计划在今后五年内生产利润每年比上一年增长20%，如果这一计划得以实现，那么该企业2003年至2008年的总利润是多少万元（精确到0.01）？

    分析 由题意，今后五年内生产利润组成以5万元为首项，1.2为公比的等比数列，利用等比数列的求和公式，即可求出该企业2003年至2008年的总利润．

    解答 解：由题意，今后五年内生产利润组成以5万元为首项，1.2为公比的等比数列，
    所以该企业2003年至2008年的总利润是$\frac{5×（1-1．{2}^{5}）}{1-1.2}$≈37.21万元．

    点评 本题考查利用数学知识解决实际问题，考查等比数列的求和公式，考查学生的计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    16．若直线a∥平面α，直线b在平面α内，则直线a与b的位置关系为（　　）
    A．一定平行B．一定异面
    C．一定相交D．可能平行、可能异面

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

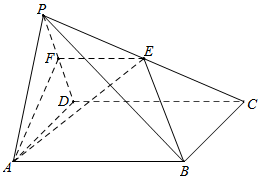    17．如图，在四棱锥P-ABCD中，底面ABCD是正方形．点E是棱PC的中点，平面ABE与棱PD交于点F．
    （Ⅰ）求证：AB∥EF；
    （Ⅱ）若PA=AD，且平面PAD⊥平面ABCD，试证明AF⊥平面PCD；
    （Ⅲ）在（Ⅱ）的条件下，线段PB上是否存在点M，使得EM⊥平面PCD？（请说明理由）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．函数f（x）=x2（x≥1）的反函数f-1（x）=$\sqrt{x}$（x≥1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．如图是根据某中学为地震灾区捐款的情况而制作的统计图，已知该校在校学生3000人，根据统计图计算该校共捐款37770元．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

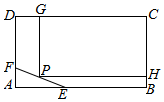    11．为了保护环境，实现城市绿化，某小区要在空地长方形ABCD上规划出一块长方形地面建造草坪CGPH，草坪一边落在CD上，一个顶点P在水池△AEF的边EF上，（如图，其中AB=200 m，BC=160m，AE=60m，AF=40m），设CG=xm，草坪的面积为f（x）．
    （1）求函数y=f（x）的解析式，并写出它的定义域；
    （2）求草坪面积的最大值，井求出此时CG的长度．（精确到整数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．在数列{an}中，若a1=3，an+1=an+n（n≥1），分别写出该数列的第2～5项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．（$\root{3}{{x}^{-1}}$-$\root{5}{{x}^{-2}}$）n展开式的所有奇数项的系数和等于1024，求展开式中二项式系数最大项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．若数列{an}满足a2-a1＞a3-a2＞a4-a3＞…＞an+1-an＞…，则称数列{an}为“差递减”数列，若数列{an}是“差递减”数列，且其通项an与其前n项和Sn（n∈N*）满足2Sn=3an+2λ-1（n∈N*），则实数λ的取值范围是$λ＞\frac{1}{2}$．

    查看答案和解析>>

    同步练习册答案