
分析 由题意先求出$\overrightarrow{a}•\overrightarrow{b}$=1,再根据向量的夹角公式计算即可.
解答 解:向量|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{3}$,
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2-2$\overrightarrow{a}•\overrightarrow{b}$=1+4-2$\overrightarrow{a}•\overrightarrow{b}$=3,
∴$\overrightarrow{a}•\overrightarrow{b}$=1,
∴cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{1}{1×2}$=$\frac{1}{2}$,
∵向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角的范围为(0,π),
∴向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,
故答案为:$\frac{π}{3}$.
点评 本题考查平面向量的数量积运算,训练了由数量积求夹角公式,是中档题.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -1+2i | B. | 1+2i | C. | 1-2i | D. | -1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
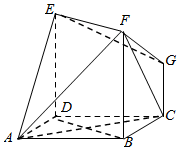 如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE=2CG=2.
如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE=2CG=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=f(x)的周期为$\frac{π}{2}$ | B. | y=f(x)在[0,$\frac{π}{6}$]上是减函数 | ||
| C. | y=f(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=f(x)是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{13}{2}$ | C. | 12 | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com