
分析 (1)根据条件利用代入法即可得f(21)+f(22)+f(23)+f(24)和g(21)+g(22)+g(23)+g(24)的值,
(2)根据分段函数的表达式,结合函数的单调性进行求解即可.
解答 解:(1)当天14点至15点这一小时内进入园区人数为f(21)+f(22)+f(23)+f(24)=360×[3${\;}^{\frac{13}{12}}$+3${\;}^{\frac{14}{12}}$+3${\;}^{\frac{15}{12}}$+3${\;}^{\frac{16}{12}}$]+3000×4≈17460(人)…3分
离开园区的人数g(21)+g(22)+g(23)+g(24)=9000 (人) …6分
(2)当f(n)-g(n)≥0 时,园内游客人数递增;
当 f(n)-g(n)<0时,园内游客人数递减.…7分
①当19≤n≤32 时,由f(n)-g(n)=360•3${\;}^{\frac{n-8}{12}}$-500n+12000≥0,可得:
当 19≤n≤28 时,进入园区游客人数多于离开园区游客人数,总人数越来越多;…9分
当29≤n≤32 时,进入园区游客人数少于离开游客人数,总人数将变少; …11分
( f(28)-g(28)=246.49>0; f(29)-g(29)=-38.13<0 )
②当33≤n≤45 时,由f(n)-g(n)=-720n+23600 递减,且其值恒为负数.进入园区游客人数少于离开游客人数,总人数将变少. …13分
综上,当天下午16点时(n=28)园区内的游客人数最多,此时计算可知园区大约共有77264人.…14分
点评 本题主要考查函数的应用问题,分析问题与解决问题的能力/能通过建立数学模型,解决有关社会生活、生产实际或其他学科的问题,并能解释其实际意义是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | α⊥β且m⊆α | B. | m⊥n且n⊆β | C. | α⊥β且m∥α | D. | m⊥n且n∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
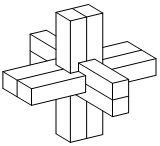 鲁班锁,是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,原为木质结构,外观看是严丝合缝的十字立方体,其上下,左右,前后完全对称,从外表上看,六根等长的正四棱柱体分成三组,经90度榫卯起来,若正四棱柱体的高为4,底面正方形的边长为1,则该鲁班锁的表面积为( )
鲁班锁,是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,原为木质结构,外观看是严丝合缝的十字立方体,其上下,左右,前后完全对称,从外表上看,六根等长的正四棱柱体分成三组,经90度榫卯起来,若正四棱柱体的高为4,底面正方形的边长为1,则该鲁班锁的表面积为( )| A. | 48 | B. | 60 | C. | 72 | D. | 84 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使ex0<x0+1成立 | B. | 对?x∈R,使2x>x2成立 | ||
| C. | a+b=0的充要条件是$\frac{a}{b}$=-1 | D. | a>1,b>1是ab>1的充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日需求量 | 3 | 4 | 5 | 6 | 7 |
| 频数 | 2 | 3 | 15 | 6 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1+2i | B. | 1+2i | C. | 1-2i | D. | -1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com