
分析 (1)求出f′(x)并令其为0得到方程,把x=-$\frac{2}{3}$和x=1代入求出a、b即可,再求出f′(x),分别令f′(x)<0,f′(x)>0,即可得到函数f(x)的单调区间;
(2)由f(0)=0,f(1)=1,得到c=0,b=-a,再求f(x)的导数,由题意可得不等式组,解不等式即可得到a的取值范围
解答 解:(1)f′(x)=3x2+2ax+b,
由题意:$\left\{\begin{array}{l}{f′(-\frac{2}{3})=0}\\{f′(1)=0}\end{array}\right.$,即 $\left\{\begin{array}{l}{3{(-\frac{2}{3})}^{2}-\frac{4}{3}a+b=0}\\{3+2a+b=0}\end{array}\right.$,
解得:a=-$\frac{1}{2}$,b=-2,
即有f(x)=x3-$\frac{1}{2}$x2-2x+c,∴f′(x)=3x2-x-2,
令f′(x)<0,解得-$\frac{2}{3}$<x<1;
令f′(x)>0,解得x<-$\frac{2}{3}$或x>1,
∴f(x)的减区间为(-$\frac{2}{3}$,1);增区间为(-∞,-$\frac{2}{3}$),(1,+∞);
(2)若f(0)=0,f(1)=1,则c=0,1+a+b+c=1,则有b=-a,c=0,
则有f(x)=x3+ax2-ax,f′(x)=3x2+2ax-a,
由于f(x)在(-2,$\frac{1}{4}$)上有极小值,
即为$\left\{\begin{array}{l}{f′(-2)>0}\\{f′(\frac{1}{4})<0}\end{array}\right.$,$\left\{\begin{array}{l}{12-4a-a>0}\\{\frac{3}{16}+\frac{1}{2}a-a<0}\end{array}\right.$,
解得:$\frac{3}{8}$<a<$\frac{12}{5}$,
则实数a的取值范围为($\frac{3}{8}$,$\frac{12}{5}$).
点评 考查学生利用导数求函数极值的能力,利用导数研究函数单调性的能力,考查二次方程实根的分布,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
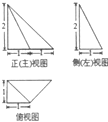
| A. | $\frac{{9+2\sqrt{3}+\sqrt{5}}}{2}$ | B. | $\frac{{9+2\sqrt{3}}}{2}$ | C. | $\frac{{9+2\sqrt{5}}}{2}$ | D. | $\frac{{11+\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为[5,15],(15,25],(25,35],(35,45],由此得到样本的重量频率分布直方图(如图).
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为[5,15],(15,25],(25,35],(35,45],由此得到样本的重量频率分布直方图(如图).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2及椭圆的短轴端点为顶点的三角形是等边三角形,椭圆的右顶点到右焦点的距离为1
已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2及椭圆的短轴端点为顶点的三角形是等边三角形,椭圆的右顶点到右焦点的距离为1查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com