
 已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2及椭圆的短轴端点为顶点的三角形是等边三角形,椭圆的右顶点到右焦点的距离为1
已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2及椭圆的短轴端点为顶点的三角形是等边三角形,椭圆的右顶点到右焦点的距离为1分析 (Ⅰ)由△AF1F2是等边三角形可得a=2c,结合椭圆的右顶点到右焦点的距离为1求得a,c的值,进一步求得b,则椭圆方程可求;
(Ⅱ)由题意设出直线l的方程,和椭圆方程联立求得M坐标,根据直线MQ⊥PM求得直线MQ的方程,求出P,Q的坐标,然后利用向量数量积为0得到PF2⊥QF2,PF1⊥QF1,再由PM⊥QM,可得点F1,Q,F2,M,P都在以PQ为直径的圆上.
解答 (Ⅰ)解:如图,∵△AF1F2是等边三角形,∴a=2c,
又∵椭圆的右顶点到右焦点的距离为1,∴a-c=1,则a=2,c=1,从而b=$\sqrt{3}$,
故椭圆E的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;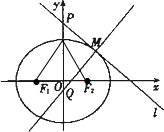 (Ⅱ)证明:依题意,直线l的斜率必存在且不为0,
(Ⅱ)证明:依题意,直线l的斜率必存在且不为0,
设直线l的方程为y=kx+m,
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=kx+m}\end{array}\right.$,得(4k2+3)x2+8mkx+4m2-12=0.
令△=0,即64m2k2-16(4k2+3)(m2-3)=0,
化简得:m2=4k2+3>0.
设M(x1,y1),则$\left\{\begin{array}{l}{{x}_{1}=-\frac{4mk}{4{k}^{2}+3}}\\{{y}_{1}=\frac{3m}{4{k}^{2}+3}}\end{array}\right.$,即$\left\{\begin{array}{l}{{x}_{1}=-\frac{4k}{m}}\\{{y}_{1}=\frac{3}{m}}\end{array}\right.$.
即M($-\frac{4k}{m},\frac{3}{m}$).
又∵直线MQ⊥PM,∴直线MQ的方程为$y-\frac{3}{m}=-\frac{1}{k}(x+\frac{4k}{m})$.
由$\left\{\begin{array}{l}{y-\frac{3}{m}=-\frac{1}{k}(x+\frac{4k}{m})}\\{x=0}\end{array}\right.$,得Q(0,$-\frac{1}{m}$),
又由$\left\{\begin{array}{l}{y=kx+m}\\{x=0}\end{array}\right.$,得P(0,m).
由(Ⅰ)知,F1(-1,0),F2(1,0),
∴$\overrightarrow{P{F}_{2}}=(1,-m),\overrightarrow{Q{F}_{2}}=(1,\frac{1}{m})$,$\overrightarrow{P{F}_{1}}=(-1,-m),\overrightarrow{Q{F}_{1}}=(-1,\frac{1}{m})$.
∴$\overrightarrow{P{F}_{2}}•\overrightarrow{Q{F}_{2}}=1+(-m)×\frac{1}{m}=0$,$\overrightarrow{P{F}_{1}}•\overrightarrow{Q{F}_{1}}=1+(-m)×\frac{1}{m}=0$.
∴PF2⊥QF2,PF1⊥QF1,
又PM⊥QM,∴点F1,Q,F2,M,P都在以PQ为直径的圆上.
故F1,Q,F2,M,P五点共圆.
点评 本题主要考查圆的方程与性质、椭圆的标准方程与性质、直线与圆锥曲线的位置关系等性质,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想、特殊与一般思想等,是难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了了解某学段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如右图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
为了了解某学段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如右图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
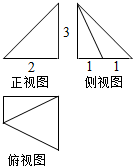
| A. | $\sqrt{14}$ | B. | $\sqrt{13}$ | C. | $\sqrt{5}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com