
分析 已知等式利用正弦定理化简,整理后利用两角和与差的正弦函数公式及诱导公式变形,求出cosA的值,确定出sinA的值,由余弦定理列出关系式,把a,cosA的值代入并利用基本不等式求出bc的最大值,利用三角形面积公式求出三角形ABC面积的最大值即可.
解答 解:已知等式(2c+b)cosA+acosB=0,
利用正弦定理化简得:(2sinC+sinB)cosA+sinAcosB=0,
整理得:2sinCcosA+sinAcosB+cosAsinB=2sinCcosA+sin(A+B)=0,
即2sinCcosA=-sin(A+B)=-sinC,
∵sinC≠0,
∴cosA=-$\frac{1}{2}$,sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{\sqrt{3}}{2}$,
由余弦定理得:a2=b2+c2-2bccosA,即16=b2+c2+bc≥2bc+bc=3bc,
∴bc≤$\frac{16}{3}$,
∴S△ABC=$\frac{1}{2}$bcsinA≤$\frac{4\sqrt{3}}{3}$,
则△ABC面积的最大值为$\frac{4\sqrt{3}}{3}$.
故答案为:$\frac{4\sqrt{3}}{3}$
点评 此题考查了正弦、余弦定理,三角形面积公式,以及基本不等式的运用,熟练掌握公式及定理是解本题的关键.


科目:高中数学 来源: 题型:选择题
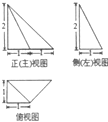
| A. | $\frac{{9+2\sqrt{3}+\sqrt{5}}}{2}$ | B. | $\frac{{9+2\sqrt{3}}}{2}$ | C. | $\frac{{9+2\sqrt{5}}}{2}$ | D. | $\frac{{11+\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2及椭圆的短轴端点为顶点的三角形是等边三角形,椭圆的右顶点到右焦点的距离为1
已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2及椭圆的短轴端点为顶点的三角形是等边三角形,椭圆的右顶点到右焦点的距离为1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)(1,+∞) | B. | (-∞,0)(1,+∞) | C. | (-∞,-1) | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com