练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．若函数y=log2（ax+1）在区间（-∞，1）上是减函数，则a的取值范围为[-1，0）．

    分析 复合函数单调性和对数性质可得a＜0且a•1+1≥0，解关于a的不等式组可得．

    解答 解：∵函数y=log2（ax+1）在区间（-∞，1）上是减函数，
    ∴y=ax+1为（-∞，1）的减函数，
    ∴a＜0且a•1+1≥0，解得-1≤a＜0，
    ∴a的取值范围为[-1，0）
    故答案为：[-1，0）

    点评 本题考查对数函数和复合函数的单调性，属基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．设全集为实数集R，函数f（x）=lg（2x-1）的定义域为A，集合B={x||x|-a≤0}（a∈R）
    （Ⅰ）若a=2，求A∪B和A∩B
    （Ⅱ）若∁RA∪B=∁RA，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知函数y=$\frac{\sqrt{2-x}}{{x}^{2}-9}$，其定义域为（　　）
    A．（-∞，2）B．（-∞，2]C．（-∞，-3）∪（-3，2]D．[2，3）∪（3，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

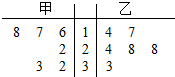    7．甲、乙两位运动员6场比赛的茎叶图如图所示，记甲、乙的平均成绩分别为$\overline{{x}_{甲}}$，$\overline{{x}_{乙}}$，下列判断正确的是（　　）
    A．$\overline{{x}_{甲}}$＞$\overline{{x}_{乙}}$，甲比乙成绩稳定B．$\overline{{x}_{甲}}$＞$\overline{{x}_{乙}}$，乙比甲成绩稳定
    C．$\overline{{x}_{甲}}$＜$\overline{{x}_{乙}}$，甲比乙成绩稳定D．$\overline{{x}_{甲}}$＜$\overline{{x}_{乙}}$，乙比甲成绩稳定

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知f（x）是定义在R上的偶函数，当x≥0时，f（x）=xa（a∈R），函数f（x）的图象经过点（4，2）．
    （1）求函数f（x）的解析式；
    （2）解不等式f（x2）-f（-x2+x-1）＞0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知方程x2+y2-2（t+3）+2（1-4t2）y+16t4+9=0，回答下列问题：
    （1）t为何值时，方程表示圆？
    （2）当方程表示圆时，t取何值时圆的面积最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．递增等比数列{an}的前n项和为Sn，a52=a10，2an+5Sn=5Sn+1-2an+2．
    （1）求an；
    （2）设bn=an|cos$\frac{nπ}{2}$|，数列{bn}的前n项和为Tn，若Tn=340，求n的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．如图所示的是北京奥运会的会徽，其中的“中国印”把它分成了5个区域，现给它着色，要求相邻区域不能用同一颜色，如果只有4种颜色可供使用，那么不同的着色方法有（　　）种．
    A．120B．72C．48D．24

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．与向量$\overrightarrow{a}$=（2，3，6）共线的单位向量是（　　）
    A．（$\frac{2}{7}$，$\frac{3}{7}$，$\frac{6}{7}$）B．（-$\frac{2}{7}$，-$\frac{3}{7}$，-$\frac{6}{7}$）
    C．（$\frac{2}{7}$，-$\frac{3}{7}$，-$\frac{6}{7}$）和（-$\frac{2}{7}$，$\frac{3}{7}$，$\frac{6}{7}$）D．（$\frac{2}{7}$，$\frac{3}{7}$，$\frac{6}{7}$）和（-$\frac{2}{7}$，-$\frac{3}{7}$，-$\frac{6}{7}$）

    查看答案和解析>>

    同步练习册答案