
分析 (Ⅰ)先求出A=($\frac{1}{2},+∞$),由a=2便可求出B=[-2,2],然后进行并集、交集的运算即可;
(Ⅱ)根据条件便有B⊆CRA,可求出${C}_{R}A=(-∞,\frac{1}{2}]$,可讨论B是否为空集:B=∅时会得到a<0;而B≠∅时得到a≥0,且B={x|-a≤x≤a},这样便可得到$0≤a≤\frac{1}{2}$,这两种情况下得到的a的范围求并集便可得出a的取值范围.
解答 解:(Ⅰ)A=$(\frac{1}{2},+∞)$;
a=2时,B=[-2,2];
∴A∪B=[-2,+∞),$A∩B=(\frac{1}{2},2]$;
(Ⅱ)∵(CRA)∪B=CRA;
∴B⊆CRA;
${C}_{R}A=(-∞,\frac{1}{2}]$;
①当B=∅时,a<0;
②当B≠∅时,B={x|-a≤x≤a}(a≥0);
∴$a≤\frac{1}{2}$,且a≥0;
∴$0≤a≤\frac{1}{2}$;
综上得,a的取值范围为$(-∞,\frac{1}{2}]$.
点评 考查函数定义域的概念及求法,对数的真数大于0,绝对值不等式的解法,交集、并集的运算,以及子集、补集的概念,不要漏了B=∅的情况.


科目:高中数学 来源: 题型:选择题
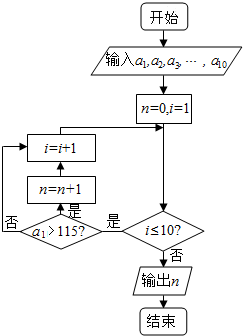 2015年11月14号,通过航拍发现河北某地焚烧秸秆比较严重,该地环保部门对11月份前十天的PM2.5(单位:μg/m3)进行监测,分别记为a1,a2,…,a10(如:a3表示11月3号的PM2.5的值),如表是11月1号至11月10号的PM2.5的监测值,根据表中的数据,下面算法流程图输出的结果为( )
2015年11月14号,通过航拍发现河北某地焚烧秸秆比较严重,该地环保部门对11月份前十天的PM2.5(单位:μg/m3)进行监测,分别记为a1,a2,…,a10(如:a3表示11月3号的PM2.5的值),如表是11月1号至11月10号的PM2.5的监测值,根据表中的数据,下面算法流程图输出的结果为( )| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| PM2.5 | 80 | 120 | 110 | 91 | 65 | 77 | 131 | 116 | 55 | 77 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com