
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
分析 由z(1+i)=i2016,得$z=\frac{{i}^{2016}}{1+i}$,然后利用复数代数形式的乘除运算化简复数z,再由复数求模公式计算即可得答案.
解答 解:由z(1+i)=i2016,
得$z=\frac{{i}^{2016}}{1+i}$=$\frac{({i}^{4})^{504}}{1+i}=\frac{1}{1+i}=\frac{1-i}{(1+i)(1-i)}=\frac{1-i}{2}$=$\frac{1}{2}-\frac{1}{2}i$.
则|z|=$\sqrt{(\frac{1}{2})^{2}+(-\frac{1}{2})^{2}}=\frac{\sqrt{2}}{2}$.
故选:B.
点评 本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:选择题
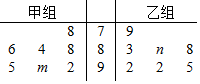 某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则m+n的值是( )
某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则m+n的值是( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在(0,$\frac{π}{4}}$)上单调递增,为奇函数 | B. | 周期为π,图象关于($\frac{π}{4},0}$)对称 | ||
| C. | 最大值为$\sqrt{2}$,图象关于直线x=$\frac{π}{2}$对称 | D. | 在(-$\frac{π}{2},0}$)上单调递增,为偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2014 | B. | 2016 | C. | 3042 | D. | 4027 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com