练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．复数z满足z（2-i）=2+i（i为虚数单位），则$\overline z$在复平面内对应的点所在象限为（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    分析 利用复数的运算法则、几何意义、共轭复数的定义即可得出．

    解答 解：∵z（2-i）=2+i，∴z（2-i）（2+i）=（2+i）（2+i），∴z=$\frac{1}{5}$（3+4i），
    则$\overline z$=$\frac{3}{5}$-$\frac{4}{5}$i在复平面内对应的点（$\frac{3}{5}$，-$\frac{4}{5}$）所在象限为第四象限．
    故选：D．

    点评 本题考查了复数的运算法则、几何意义、共轭复数的定义，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．已知集合A={x|x2-x＞0}，$B=\left\{{x\left|{-\sqrt{3}＜x＜\sqrt{3}}\right.}\right\}$，则（　　）
    A．A∩B=∅B．A∪B=RC．B⊆AD．A⊆B

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．在直角坐标系xOy中，以坐标原点为极点，以x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=2$\sqrt{2}$sinθ．
    （Ⅰ）将曲线C的极坐标方程化为参数方程：
    （Ⅱ）如果过曲线C上一点M且斜率为-$\sqrt{3}$的直线与直线l：y=-x+6交于点Q，那
    么当|MQ|取得最小值时，求M点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

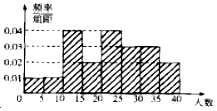    3．为了更好地让学生适应高考网上阅卷，某学校针对该校20个班级进行了“汉字与英语书法大赛”（每个班级只有一个指导老师），并调查了各班参加该比赛的学生人数，根据所得数据，分组成[0，5），[5，10），[10，15），[15，20），[20，25），[25，30），[30，35），[35，40]时，所作的频率分布直方图如图：
    （1）如果从参加比赛的学生人数在25人以上（含25人）的班级中随机选取2个指导老师颁发“参与组织奖”，那么至少有一位来自“参与学生人数在[25，30）内的班级”的指导老师获奖的概率是多少？
    （2）如果从参加比赛的学生人数在25人以上（含25人）的班级中随机选取3个指导老师颁发“参与组织奖”，设“参与学生人数在[25，30）内的班级”的指导老师获奖人数为X，求随机变量X的分布列和数学期望E（X）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．过点A（1，t）于曲线y=x3-12x相切的直线有3条，则实数t的取值范围为（-12，-11）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知x，y满足约束条件$\left\{\begin{array}{l}{x-y+1≤0}\\{2x+y-a≥0}\\{y-2≤0}\end{array}\right.$，若目标函数z=x-2y的最大值是-2，则实数a=（　　）
    A．-6B．-1C．1D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知集合A={x|x2+3x≤0}，集合B={n|n=2k+1，k∈Z}，则A∩B=（　　）
    A．{-1，1}B．{1，3}C．{-3，-1}D．{-3，-1，1，3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知2sinα•tanα=3，且0＜α＜π．
    （1）求α的值；
    （2）求函数f（x）=4sinxsin（x-α）在$[0，\frac{π}{4}]$上的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知集合A={3，a2}，B={2，1-a，b}，且A∩B={1}，则A∪B=（　　）
    A．{0，1，3}B．{1，2，3}C．{1，2，4}D．{0，1，2，3}

    查看答案和解析>>

    同步练习册答案