
分析 (Ⅰ)根据ρcosθ=x,ρsinθ=y,ρ2=x2+y2化为普通方程,再转化为参数方程即可.
(Ⅱ)设斜率为$-\sqrt{3}$的直线与l的夹角为γ(定值),M到l的距离为d,令$M(\sqrt{2}cosα\;,\sqrt{2}+\sqrt{2}sinα)$,则$d=\frac{{|2sin(α+\frac{π}{4})+\sqrt{2}-6|}}{{\sqrt{2}}}$,利用三角函数的有界限求解最小值即可.
解答 解:(Ⅰ)∵$ρ=2\sqrt{2}sinθ$,∴${ρ^2}=2\sqrt{2}ρsinθ$,
∵ρcosθ=x,ρsinθ=y,ρ2=x2+y2,
∴曲线C的普通方程为${x^2}+{y^2}-2\sqrt{2}y=0$,
∴曲线C的参数方程为$\left\{\begin{array}{l}x=\sqrt{2}cosα\\ y=\sqrt{2}+\sqrt{2}sinα\end{array}\right.$(α为参数).
(Ⅱ)方法一:设斜率为$-\sqrt{3}$的直线与l的夹角为γ(定值),M到l的距离为d,
则 $|MQ|=\frac{d}{sinγ}$,所以d取最小值时,|MQ|最小.
令$M(\sqrt{2}cosα\;,\sqrt{2}+\sqrt{2}sinα)$,则$d=\frac{{|2sin(α+\frac{π}{4})+\sqrt{2}-6|}}{{\sqrt{2}}}$,
当$α=\frac{π}{4}$时,d最小.
∴点M的坐标为$M(1,\sqrt{2}+1)$.
(Ⅱ)方法二:设斜率为$-\sqrt{3}$的直线与l的夹角为γ(定值),M到l的距离为d,
则 $|MQ|=\frac{d}{sinγ}$,
∴d取最小值时,|MQ|最小.
∴,M是过圆心垂直于l的直线$y=x+\sqrt{2}$与圆(靠近直线l端)的交点.
由$\left\{\begin{array}{l}{x^2}+{(y-\sqrt{2})^2}=2\;\\ y=x+\sqrt{2}\;\end{array}\right.$,得$\left\{\begin{array}{l}x=1\;\\ y=\sqrt{2}+1\;\end{array}\right.$或$\left\{\begin{array}{l}x=-1\;\\ y=\sqrt{2}-1\;\end{array}\right.$(舍去).
∴点M的坐标为$M(1,\sqrt{2}+1)$.
点评 本题考查参数方程、极坐标方程、普通方程的互化,以及应用,直线参数方程的几何意义的运用.属于中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
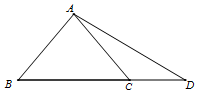 如图,△ABC是等腰直角三角形,∠bac=90°,点D在边BC的延长线上,且BC=2CD,$AD=\sqrt{5}$.
如图,△ABC是等腰直角三角形,∠bac=90°,点D在边BC的延长线上,且BC=2CD,$AD=\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com