
分析 设等差数列{an}的公差为d(d≥0),数列$\left\{{\sqrt{S_n}}\right\}$为等差数列,取前3项成等差数列,解方程可得d=2,运用等差数列的通项公式和求和公式,可得an,求得bn=$\frac{{a}_{n+2}}{{2}^{n}•{a}_{n}•{a}_{n+1}}$=$\frac{2n+3}{{2}^{n}•(2n-1)•(2n+1)}$=$\frac{1}{{2}^{n-1}•(2n-1)}$-$\frac{1}{{2}^{n}•(2n+1)}$,运用数列的求和方法:裂项相消求和,化简整理即可得到所求和.
解答 解:设等差数列{an}的公差为d(d≥0),
∵$\sqrt{S_1}=1$,$\sqrt{S_2}=\sqrt{2+d}$,$\sqrt{S_3}=\sqrt{3+3d}$成等差数列,
∴$2\sqrt{2+d}=1+\sqrt{3+3d}$,解得d=2,
∴an=1+(n-1)×2=2n-1,
Sn=$\frac{n(1+2n-1)}{2}$=n2,$\sqrt{{S}_{n}}$=n,故数列$\left\{{\sqrt{S_n}}\right\}$为等差数列,
bn=$\frac{{a}_{n+2}}{{2}^{n}•{a}_{n}•{a}_{n+1}}$=$\frac{2n+3}{{2}^{n}•(2n-1)•(2n+1)}$
=$\frac{1}{{2}^{n-1}•(2n-1)}$-$\frac{1}{{2}^{n}•(2n+1)}$,
则前n项和Tn=$\frac{1}{{2}^{0}•1}$-$\frac{1}{{2}^{1}•3}$+$\frac{1}{{2}^{1}•3}$-$\frac{1}{{2}^{2}•5}$+…+$\frac{1}{{2}^{n-1}•(2n-1)}$-$\frac{1}{{2}^{n}•(2n+1)}$
=1-$\frac{1}{{2}^{n}•(2n+1)}$.
故答案为:1-$\frac{1}{{2}^{n}•(2n+1)}$.
点评 本题考查等差数列的通项公式和求和公式的运用,考查数列的求和方法:裂项相消求和,以及化简整理的运算能力,属于中档题,


科目:高中数学 来源: 题型:选择题
| A. | $[0,\frac{3π}{4}]$ | B. | $[0,\frac{π}{2})∪[\frac{3π}{4},π)$ | C. | $[\frac{3π}{4},π)$ | D. | $(\frac{π}{2},\frac{3π}{4}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}-1}}{2}$ | B. | $\frac{{\sqrt{3}-1}}{2}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{\sqrt{5}-\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
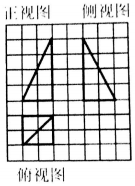 如图所示,网格纸上小正方形的边长为1,粗线画出的是某一几何体的三视图,则该几何体外接球的表面积为( )
如图所示,网格纸上小正方形的边长为1,粗线画出的是某一几何体的三视图,则该几何体外接球的表面积为( )| A. | 8π | B. | 16π | C. | 20π | D. | 24π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
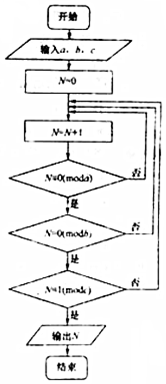 若正整数N除以正整m后的余数为n,则记为N=n(modm),例如10=4(mod6).如图程序框图的算法源于我国古代《孙子算经》中的“孙子定律”的某一环节,执行该框图,输入a=2,b=3,c=5,则输出的N=( )
若正整数N除以正整m后的余数为n,则记为N=n(modm),例如10=4(mod6).如图程序框图的算法源于我国古代《孙子算经》中的“孙子定律”的某一环节,执行该框图,输入a=2,b=3,c=5,则输出的N=( )| A. | 6 | B. | 9 | C. | 12 | D. | 21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com