
| A. | $[0,\frac{3π}{4}]$ | B. | $[0,\frac{π}{2})∪[\frac{3π}{4},π)$ | C. | $[\frac{3π}{4},π)$ | D. | $(\frac{π}{2},\frac{3π}{4}]$ |
分析 求出函数的导函数,由导函数的值域得到切线倾斜角正切值的范围,则倾斜角的范围可求.
解答 解:由函数$f(x)=\frac{1}{3}{x^3}-{x^2}$,得f′(x)=x2-2x,
设函数$f(x)=\frac{1}{3}{x^3}-{x^2}$图象上任一点P(x0,y0),且过该点的切线的倾斜角为α(0≤α<π),
则f′(x)=x2-2x=(x-1)2-1≥-1,
∴tanα≥-1,
∴0≤α<$\frac{π}{2}$或$\frac{3π}{4}$≤α<π.
∴过函数$f(x)=\frac{1}{3}{x^3}-{x^2}$图象上一个动点作函数的切线,切线倾斜角的范围为[0,$\frac{π}{2}$)∪[$\frac{3π}{4}$,π).
故选B.
点评 本题考查导数的几何意义,考查直线倾斜角和斜率的关系,关键是熟练掌握正切函数的单调性,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨(¬q) | C. | p∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>c>a | B. | c>b>a | C. | b>a>c | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
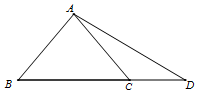 如图,△ABC是等腰直角三角形,∠bac=90°,点D在边BC的延长线上,且BC=2CD,$AD=\sqrt{5}$.
如图,△ABC是等腰直角三角形,∠bac=90°,点D在边BC的延长线上,且BC=2CD,$AD=\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1008 | B. | 1010 | C. | 2016 | D. | 2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1190秒 | B. | 1195秒 | C. | 1200秒 | D. | 1205秒 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com