
分析 (Ⅰ)设等差数列{an}的公差为d(d≥0),由数列{$\sqrt{{S}_{n}}$}也为等差数列可得$2\sqrt{{S}_{2}}=\sqrt{{S}_{1}}+\sqrt{{S}_{3}}$,由此求出等差数列的公差,验证数列{$\sqrt{{S}_{n}}$}也为等差数列,则等差数列{an}的通项公式可求;
(Ⅱ)把(Ⅰ)中求得的通项公式与前n项和公式代入bn=$\frac{{a}_{n+1}}{{S}_{n}•{S}_{n+1}}$,利用裂项相消法求得数列{bn}的前n项和.
解答 解:(Ⅰ)设等差数列{an}的公差为d(d≥0),
∵a1=1,an>0,∴$\sqrt{{S}_{2}}=\sqrt{2+d}$,$\sqrt{{S}_{3}}=\sqrt{3+3d}$成等差数列,
则2$\sqrt{2+d}=1+\sqrt{3+3d}$,解得:d=2,
∴an=1+2(n-1)=2n-1,
则${S}_{n}=n+\frac{n(n-1)}{2}×2={n}^{2}$,
∴数列$\sqrt{{S}_{n}}$=n为等差数列,
∴an=2n-1;
(Ⅱ)由(Ⅰ),an+1=2n+1,${S}_{n}={n}^{2}$,
∴bn=$\frac{{a}_{n+1}}{{S}_{n}•{S}_{n+1}}$=$\frac{2n+1}{{n}^{2}•(n+1)^{2}}=\frac{1}{{n}^{2}}-\frac{1}{(n+1)^{2}}$,
设数列{bn}的前n项和为Tn,则
${T}_{n}=(\frac{1}{{1}^{2}}-\frac{1}{{2}^{2}})+(\frac{1}{{2}^{2}}-\frac{1}{{3}^{2}})+…+(\frac{1}{{n}^{2}}-\frac{1}{(n+1)^{2}})$=$1-\frac{1}{(n+1)^{2}}=\frac{{n}^{2}+2n}{(n+1)^{2}}$.
点评 本题考查数列的求和,训练了裂项相消法求数列的前n项和,属中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
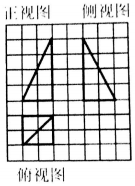 如图所示,网格纸上小正方形的边长为1,粗线画出的是某一几何体的三视图,则该几何体外接球的表面积为( )
如图所示,网格纸上小正方形的边长为1,粗线画出的是某一几何体的三视图,则该几何体外接球的表面积为( )| A. | 8π | B. | 16π | C. | 20π | D. | 24π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
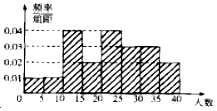 为了更好地让学生适应高考网上阅卷,某学校针对该校20个班级进行了“汉字与英语书法大赛”(每个班级只有一个指导老师),并调查了各班参加该比赛的学生人数,根据所得数据,分组成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]时,所作的频率分布直方图如图:
为了更好地让学生适应高考网上阅卷,某学校针对该校20个班级进行了“汉字与英语书法大赛”(每个班级只有一个指导老师),并调查了各班参加该比赛的学生人数,根据所得数据,分组成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]时,所作的频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1} | B. | {1,3} | C. | {-3,-1} | D. | {-3,-1,1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com