
 在△ABC中,如图,∠C=90°,AC=6,BC=8,设直线l与斜边AB交于点E,与直角边交于点F.设AE=x,是否存在直线l同时平分△ABC的周长和面积?若存在直线l,求出x的值,若不存在直线l,请说明理由.
在△ABC中,如图,∠C=90°,AC=6,BC=8,设直线l与斜边AB交于点E,与直角边交于点F.设AE=x,是否存在直线l同时平分△ABC的周长和面积?若存在直线l,求出x的值,若不存在直线l,请说明理由. 分析 根据AE=x得到AF,然后表示三角形AEF的面积,列出两个变量之间的关系式即可得出结论.
解答 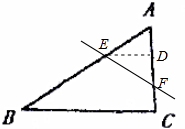 解:在直角三角形ABC中,∠C=90°,AC=6,BC=8,所以AB=10.
解:在直角三角形ABC中,∠C=90°,AC=6,BC=8,所以AB=10.
∴三角形ABC的周长为24,又因EF平分三角形ABC的周长,
∴AE+AF=12,
而AE=x,
∴AF=12-x
过点E作ED⊥AC于D,
则$\frac{DE}{AE}$=sinA=$\frac{4}{5}$,∴DE=$\frac{4}{5}$x,
∴S△AEF=$\frac{1}{2}×\frac{4}{5}x(12-x)=\frac{1}{2}×6×8$,
∴x2-12x+60=0,方程无解,
∴不存在直线l同时平分△ABC的周长和面积.
点评 本题考查了一元二次方程的应用及根据实际问题列出二次函数关系式,解题的关键是根据已知条件表示出有关的线段的长.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
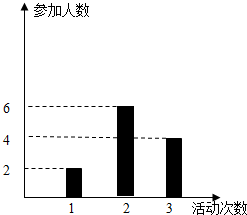 某城市号召中学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该城市某学校学生会共有12名学生,他们参加活动的次数统计如图所示.
某城市号召中学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该城市某学校学生会共有12名学生,他们参加活动的次数统计如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
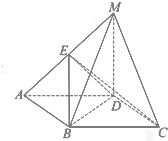 如图,四棱锥M-ABCD中,底面ABCD为矩形,MD⊥平面ABCD,且MD=DA=1,E为MA中点.
如图,四棱锥M-ABCD中,底面ABCD为矩形,MD⊥平面ABCD,且MD=DA=1,E为MA中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com