
分析 分别求出从甲箱中摸出一个白球的概率为$\frac{3}{5}$,从乙箱中摸出一个白球的概率为$\frac{1}{2}$,根据互斥事件的概率公式计算,然后判断即可.
解答 解:我认为获奖的概率小于0.5.理由如下:
甲箱子里有3个白球,2个黑球,从甲箱中摸出一个白球的概率为$\frac{3}{5}$,
乙箱子里有2个白球,2个黑球,从乙箱中摸出一个白球的概率为$\frac{2}{4}$=$\frac{1}{2}$,
故从这两个箱子里分别摸出1个球,它们都是白球的概率P=$\frac{3}{5}$×$\frac{1}{2}$=$\frac{3}{10}$,
故获奖的概率为$\frac{3}{10}$$<\frac{1}{2}$,
即获奖的概率小于0.5.
点评 本题考查了独立事件同时发生的概率,为两事件的概率的乘积,属于基础题.


科目:高中数学 来源: 题型:解答题
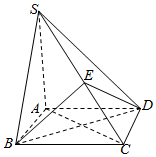 如图,四棱锥S-ABCD的底面是正方形,SA⊥底面ABCD,E是SC上一点.
如图,四棱锥S-ABCD的底面是正方形,SA⊥底面ABCD,E是SC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
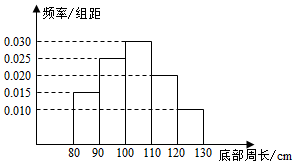
| A. | 105,115 | B. | 105,105 | C. | 105,$\frac{310}{3}$ | D. | 115,115 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com