Question

11．已知多面体ABCDFE的每个顶点都在球O的表面上，四边形ABCD为正方形，EF∥BD，且E，F在平面ABCD内的射影分别为B，D，若△ABE的面积为2，则球O的表面积的最小值为（　　）

• A． 8$\sqrt{2}$π
• B． 8π
• C． 12$\sqrt{2}$π
• D． 12π

Answer 1

分析 由题意求出AB、BE的长，然后把多面体补形为长方体，写出其外接球的表面积，利用基本不等式求最值．

解答 解：设AB=a，BE=b，则△ABE的面积为$\frac{1}{2}ab=2$，∴ab=4，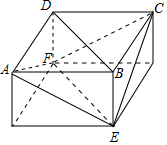
多面体EFABCD可以通过补形为长方体，如图所示：
则球O即为该长方体的外接球，
其表面积为$4π×（\frac{\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}}{2}）^{2}$=$π×（2{a}^{2}+{b}^{2}）≥2π\sqrt{2{a}^{2}{b}^{2}}=2\sqrt{2}πab$=$8\sqrt{2}π$．
故选：A．

点评 本题考查球的表面积与体积，考查数学补形思想方法，是中档题．