Question

6．解不等式：（1）$\frac{3x-2}{2x}≥1$；（2）$\frac{{x}^{2}-x-2}{{x}^{2}+5x+6}＜0$．

Answer 1

分析 （1）$\frac{3x-2}{2x}≥1$移项，通分，利用同号得正求解即可或者转化为二次不等式的解法；
（2）分子分母因式分解，利用标根法求解即可．

解答 解：：（1）$\frac{3x-2}{2x}≥1$；
可得：$\frac{3x-2}{2x}-1≥0$；即$\frac{x-2}{2x}≥0$，
∴2x（x-2）≥0，且x≠0．
解得：x≥2或x＜0，
∴原不等式的解集为{x|x≥2或x＜0}．
（2）$\frac{{x}^{2}-x-2}{{x}^{2}+5x+6}＜0$．
原不等式化简为：$\frac{（x-2）（x+1）}{（x+2）（x+3）}＜0$，
转化为整数不等式：（x+3）（x+2）（x+1）（x-2）＜0．
令：x+3）（x+2）（x+1）（x-2）=0．
可得方程的根x₁=-3，x₂=-2，x₃=-1，x₄=2．
标根穿线：小于0，取下部分．分母不能取等．
∴原不等式的解集为{x|2＞x＞-1或-3＜x＜-2}．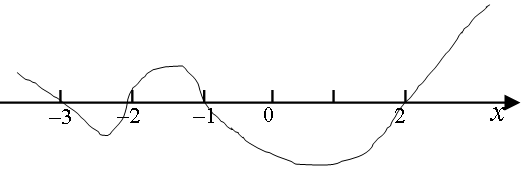

点评 本题考查不等式的解法，主要考查高次不等式的解法注意转化为整式不等式，考查运算能力，属于基础题．