
已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.
(1) 求与圆C相切,且与直线l垂直的直线方程;
(2) 在直线OA上(O为坐标原点),存在定点B(不同于点A),满足:对于圆C上任一点P,都有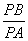 为一常数,试求所有满足条件的点B的坐标.
为一常数,试求所有满足条件的点B的坐标.

解:(1) 设所求直线方程为y=-2x+b,即2x+y-b=0,
∵ 直线与圆相切,∴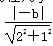 =3,得b=±3
=3,得b=±3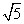 ,∴ 所求直线方程为y=-2x±3
,∴ 所求直线方程为y=-2x±3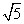 .
.
(2) (解法1)假设存在这样的点B(t,0),
当P为圆C与x轴左交点(-3,0)时,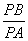 =
=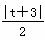 ;
;
当P为圆C与x轴右交点(3,0)时,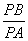 =
=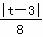 ,
,
依题意,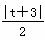 =
=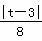 ,解得,t=-5(舍去),或t=-
,解得,t=-5(舍去),或t=-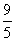 .
.
下面证明点B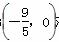 对于圆C上任一点P,都有
对于圆C上任一点P,都有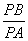 为一常数.
为一常数.
设P(x,y),则y2=9-x2,
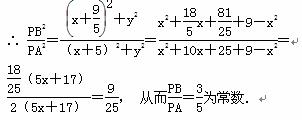 (解法2)假设存在这样的点B(t,0),使得
(解法2)假设存在这样的点B(t,0),使得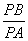 为常数λ,则PB2=λ2PA2,∴ (x-t)2+y2=λ2[(x+5)2+y2],将y2=9-x2代入得,x2-2xt+t2+9-x2=λ2(x2+10x+25+9-x2),即
为常数λ,则PB2=λ2PA2,∴ (x-t)2+y2=λ2[(x+5)2+y2],将y2=9-x2代入得,x2-2xt+t2+9-x2=λ2(x2+10x+25+9-x2),即
2(5λ2+t)x+34λ2-t2-9=0对x∈[-3,3]恒成立,
∴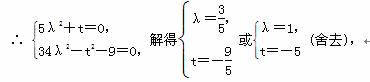
所以存在点B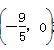 对于圆C上任一点P,都有
对于圆C上任一点P,都有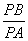 为常数
为常数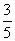 .
.


科目:高中数学 来源: 题型:
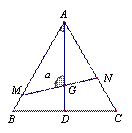
如图, 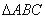 是边长为1的正三角形,
是边长为1的正三角形,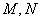 分别是边
分别是边 上的点,线段
上的点,线段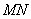 过
过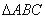 的重心
的重心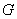 ,设
,设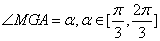 .
.
(1)当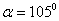 时,求
时,求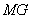 的长;
的长;
(2) 分别记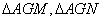 的面积为
的面积为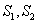 ,试将
,试将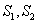 表示为
表示为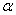 的函数;
的函数;
(3)求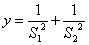 的最大值和最小值。
的最大值和最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C: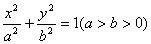 ,离心率
,离心率 ,短轴顶点为A,B,过点P(0,2)的直线为
,短轴顶点为A,B,过点P(0,2)的直线为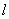 ,当直线
,当直线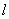 与椭圆C相切时,切点为
与椭圆C相切时,切点为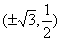 。
。
(1)求椭圆C的方程
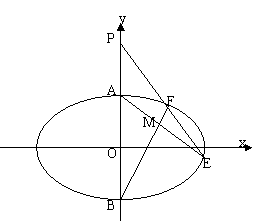
(2)若直线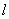 与椭圆C交于两点E,F时,连接AE,BF(如图)交于点为M,证明:点M是否在定直线上,若是,求出该直线,若不是,说明理由。
与椭圆C交于两点E,F时,连接AE,BF(如图)交于点为M,证明:点M是否在定直线上,若是,求出该直线,若不是,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆M过两点A(1,-1),B(-1,1),且圆心M在x+y-2=0上.
(1) 求圆M的方程;
(2) 设P是直线3x+4y+8=0上的动点,PA′、PB′是圆M的两条切线,A′、B′为切点,求四边形PA′MB′面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列关于互不相同的直线l、m、n和平面α、β、γ的三个命题:
①若l与m为异面直线,l⊂α,m⊂β,则α∥β; ②若α∥β,l⊂α,m⊂β,则l∥m;
③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.
其中真命题的个数为 ( )
A.3 B.2 C.1 D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
α、β是两个不同的平面,m、n是平面α、β外的两条不同直线,给出四个结论:
①m⊥n; ②α⊥β; ③n⊥β; ④m⊥α.
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题______
查看答案和解析>>
科目:高中数学 来源: 题型:
现有4名教师参加说课比赛,共有4道备选题目,若每位教师从中有放回地随机选出一道题目进行说课,其中恰有一道题目没有被这4位教师选中的情况有( )
A.288种 B.144种 C.72种 D.36种
查看答案和解析>>
科目:高中数学 来源: 题型:
将平面向量的数量积运算与实数的乘法运算相类比,易得下列结论:
(1)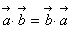
(2)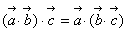
(3)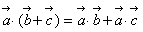
(4)由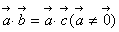 可得
可得
以上通过类比得到的结论正确的有:( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com