
分析 分n=1与n≥2讨论可得$\frac{n}{{a}_{n}}$=32n-1,从而可得$\frac{{a}_{n}}{n}$=31-2n,化简bn=1-2n,从而由裂项求和的方法求前n项和即可.
解答 解:当n=1时,$\frac{1}{{a}_{1}}$=3,
当n≥2,n∈N*时,
$\frac{1}{{a}_{1}}$+$\frac{2}{{a}_{2}}$+…+$\frac{n}{{a}_{n}}$=$\frac{3}{8}$(32n-1)①,
$\frac{1}{{a}_{1}}$+$\frac{2}{{a}_{2}}$+…+$\frac{n-1}{{a}_{n-1}}$=$\frac{3}{8}$(32n-2-1)②;
①-②得,
$\frac{n}{{a}_{n}}$=$\frac{3}{8}$(32n-1-(32n-2-1))=32n-1,
$\frac{1}{{a}_{1}}$=3也成立,
故$\frac{n}{{a}_{n}}$=32n-1,
故$\frac{{a}_{n}}{n}$=31-2n,
故bn=log3$\frac{a_n}{n}$=log331-2n=1-2n,
故$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{(1-2n)(-1-2n)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$);
故$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+…+$\frac{1}{{b}_{n}{b}_{n+1}}$
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$.
故答案为:$\frac{n}{2n+1}$.
点评 本题考查了前n项和与等比数列的通项公式的求法及裂项求和法的应用,属于中档题.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
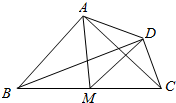 如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )
如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )| A. | 1 | B. | -1 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3+i | B. | 3-i | C. | $\frac{3}{10}$i+$\frac{1}{10}$ | D. | $\frac{3}{10}$+$\frac{1}{10}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com