
分析 (1)将|k$\overrightarrow a$+$\overrightarrow b$|=$\sqrt{3}$|$\overrightarrow a$-k$\overrightarrow b$|两边平方化简即可得出$\overrightarrow{a}•\overrightarrow{b}$,利用基本不等式求出$\overrightarrow{a}•\overrightarrow{b}$的最小值即可得出夹角的最大值;
(2)令$\overrightarrow{a}•\overrightarrow{b}$=±1,解方程得出k.
解答 解:(1)∵|k$\overrightarrow a$+$\overrightarrow b$|=$\sqrt{3}$|$\overrightarrow a$-k$\overrightarrow b$|,∴(k$\overrightarrow{a}$+$\overrightarrow{b}$)2=3($\overrightarrow{a}$-k$\overrightarrow{b}$)2,
即k2${\overrightarrow{a}}^{2}$+2k$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=3${\overrightarrow{a}}^{2}$-6k$\overrightarrow{a}•\overrightarrow{b}$+3k2$\overrightarrow{b}$2,
∴8k$\overrightarrow{a}•\overrightarrow{b}$=2k2+2,
∴$\overrightarrow{a}•\overrightarrow{b}$=$\frac{{k}^{2}+1}{4k}$,
∵$\frac{{k}^{2}+1}{4k}$=$\frac{1}{4}$(k+$\frac{1}{k}$)≥$\frac{1}{2}$,当且仅当k=$\frac{1}{k}$即k=1时取等号.
∴当$\overrightarrow{a}•\overrightarrow{b}$=cosθ=$\frac{1}{2}$时,θ取得最大值.
∴$\overrightarrow a$与$\overrightarrow b$的夹角θ的最大值为$\frac{π}{3}$.
(2)∵$\overrightarrow a∥\overrightarrow b$,
∴$\overrightarrow a$与$\overrightarrow b$夹角为0°或180°,
∴$\overrightarrow{a}•\overrightarrow{b}$=cosθ=±1,
∴$\frac{{k}^{2}+1}{4k}$=±1,解的k=±2$±\sqrt{3}$.
又∵k>0,
∴k=2±$\sqrt{3}$.
点评 本题考查了平面向量的数量积运算,不等式的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
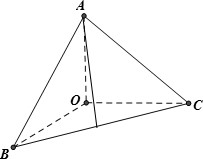 如图所示,在三棱锥A-OBC中,OA,OB,OC两两垂直且长度都为2,则这个三棱锥的体积为$\frac{4}{3}$;O到平面ABC的距离为$\frac{2\sqrt{3}}{3}$.
如图所示,在三棱锥A-OBC中,OA,OB,OC两两垂直且长度都为2,则这个三棱锥的体积为$\frac{4}{3}$;O到平面ABC的距离为$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n⊥α,则m∥n | ||
| C. | 若m∥α,n∥α,β∥α,则m∥n | D. | 若m∥n,m∥α,则n∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com