
分析 (1)利用函数的导数和斜率的关系以及函数值,列出方程组,即可求a,b的值;
(2)设g(x)=f(x)-(2x-2)=2-x-x2+3ln x,求出函数的导数,判断函数的单调性,求出函数的最值,然后证明f(x)≤2x-2对任意正实数x恒成立.
解答 (1)解:由题设,y=f(x)在点P(1,0)处切线的斜率为2.
∴$\left\{{\begin{array}{l}{f(1)=1+a=0}\\{f'(1)=1+2a+b=2}\end{array}}\right.$,解之得$\left\{{\begin{array}{l}{a=-1}\\{b=3}\end{array}}\right.$(6分)
因此实数a,b的值分别为-1和3.
(2)证明:f(x)=x-x2+3lnx(x>0).
设g(x)=f(x)-(2x-2)=2-x-x2+3ln x,
则g′(x)=-1-2x+$\frac{3}{x}$=-$\frac{(x-1)(2x+3)}{x}$.
当0<x<1时,g′(x)>0;当x>1时,g′(x)<0.
∴g(x)在 (0,1)上单调递增;在(1,+∞)上单调递减.
∴g(x)在x=1处有最大值g(1)=0,
∴f(x)-(2x-2)≤0,即f(x)≤2x-2,得证.(12分)
点评 本题考查函数的导数的综合应用,利用导数研究函数切线及最值,考查转化思想以及计算能力.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
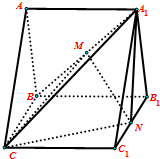 在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.M、N分别为A1B、B1C1中点.
在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.M、N分别为A1B、B1C1中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com