
分析 由题设分别求出a1,a2,a3,a4,a5,a6,a7,a8,a9,仔细观察能够发现{an}从第3项开始是周期为6的周期数列,故a2016=a6=98,当n>m且an为奇数时,an恒为常数p,知an=p,an+1=3p+5,an+2=$\frac{3p+5}{{2}^{k}}$,再由数列{an}的各项均为正整数,能求出p.
解答 解:由题设知,a1=11,
a2=3×11+5=38,
a3=$\frac{38}{2}$=19,
a4=3×19+5=62,
a5=$\frac{62}{2}$=31,
a6=3×31+5=98,
a7=$\frac{98}{2}$49,
a8=3×49+5=152,
a9=$\frac{152}{{2}^{3}}$=19,
∴{an}从第3项开始是周期为6的周期数列,
a2016=a6=98,
若存在m∈N*,当n>m且an为奇数时,an恒为常数p,
则an=p,an+1=3p+5,an+2=$\frac{3p+5}{{2}^{k}}$,
∴(3-2k)p=-5,
∵数列{an}的各项均为正整数,
∴当k=2时,p=5,
当k=3时,p=1.
故答案为:98,1或5.
点评 题考查数列的递推公式的性质和应用,解题时分别求出a1,a2,a3,…,a8,a9,仔细观察能够发现{an}从第3项开始是周期为6的周期数列,借助数列的周期性进行求解,属于中档题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
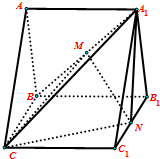 在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.M、N分别为A1B、B1C1中点.
在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.M、N分别为A1B、B1C1中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
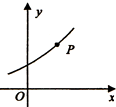 已知函数y=ax+b(b>0)的图象经过点P(1,2),如图所示,则$\frac{4}{a-1}$+$\frac{1}{b}$的最小值为3.
已知函数y=ax+b(b>0)的图象经过点P(1,2),如图所示,则$\frac{4}{a-1}$+$\frac{1}{b}$的最小值为3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{3}{4}$π,$\frac{π}{4}$] | B. | [-π,0] | C. | [-$\frac{π}{4}$,$\frac{3}{4}$π] | D. | [-$\frac{π}{2}$,$\frac{π}{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com