
分析 (Ⅰ)由{${\frac{S_n}{n}}$}是等差数列,且a1=3,$\frac{S_2}{2}$+$\frac{S_3}{3$+$\frac{S_4}{4}$=15,得到等差数列的公差,求得等差数列的通项公式,进一步求得Sn,再由an=Sn-Sn-1即可得出数列{an}的通项公式;
(Ⅱ)由a1=3,an=2n+1,得Sn=n(n+2).则n为奇数,cn=$\frac{2}{{S}_{n}}$=$\frac{2}{n(n+2)}=\frac{1}{n}-\frac{1}{n+2}$,n为偶数,cn=${2}^{{a}_{\frac{n}{2}}}$=2n+1.然后分组求和,利用裂项求和及等比数列的前n项和公式即可得出T2n.
解答 解:(Ⅰ)∵{${\frac{S_n}{n}}$}是等差数列,a1=3,$\frac{S_2}{2}$+$\frac{S_3}{3$+$\frac{S_4}{4}$=15,
∴3×$\frac{{S}_{3}}{3}=15$,即$\frac{{S}_{3}}{3}=5$.
∴$\frac{{S}_{3}}{3}$=$\frac{{S}_{1}}{1}$+d(3-1),即5=3+2d,解得d=1.
∴$\frac{{S}_{n}}{n}=3+1×(n-1)=n+2$,
∴Sn=n2+2n.
∴an=Sn-Sn-1=n2+2n-(n-1)2-2(n-1)=2n+1(n≥2),
当n=1时,也成立.
∴an=2n+1;
(Ⅱ)由a1=3,an=2n+1,得Sn=n(n+2),
则n为奇数时,cn=$\frac{2}{{S}_{n}}$=$\frac{2}{n(n+2)}=\frac{1}{n}-\frac{1}{n+2}$,
n为偶数时,∵an=2n+1,
∴${a}_{\frac{n}{2}}=2×\frac{n}{2}+1=n+1$,
则cn=${2}^{{a}_{\frac{n}{2}}}$=2n+1.
∴T2n=(c1+c3+…+c2n-1)+(c2+c4+…+c2n)
=[(1-$\frac{1}{3}$)+($\frac{1}{3}-\frac{1}{5}$)+…+($\frac{1}{2n-1}-\frac{1}{2n+1}$)]+(23+25+…+22n+1)
=1-$\frac{1}{2n+1}$+$\frac{8(1-{4}^{n})}{1-4}$=$\frac{2n}{2n+1}+\frac{8}{3}({4}^{n}-1)$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“分组求和”、“裂项求和”,考查了推理能力与计算能力,属于中档题.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | |z|=2 | B. | $\overline{z}$=1-i | C. | z的实部为1 | D. | z+1为纯虚数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某班m名学生在一次考试中数学成绩的频率分布直方图如图,若在这m名学生中,数学成绩不低于100分的人数为33,则m等于( )
某班m名学生在一次考试中数学成绩的频率分布直方图如图,若在这m名学生中,数学成绩不低于100分的人数为33,则m等于( )| A. | 45 | B. | 48 | C. | 50 | D. | 55 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2+$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{6}$或$\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
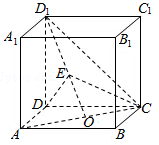 已知正方体ABCD-A1B1C1D1的棱长为2,O是AC的中点,E是线段D1O上一点,且$\overrightarrow{{D_1}E}=λ\overrightarrow{EO}$.
已知正方体ABCD-A1B1C1D1的棱长为2,O是AC的中点,E是线段D1O上一点,且$\overrightarrow{{D_1}E}=λ\overrightarrow{EO}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com