
分析 (Ⅰ)x=$\frac{π}{3}$时,可以求出向量$\overrightarrow{a}$的坐标,然后根据$cos<\overrightarrow{a},\overrightarrow{c}>=\frac{\overrightarrow{a}•\overrightarrow{c}}{|\overrightarrow{a}||\overrightarrow{c}|}$即可求出$cos<\overrightarrow{a},\overrightarrow{c}>$,从而可以得出向量$\overrightarrow{a},\overrightarrow{c}$的夹角;
(Ⅱ)进行向量数量积的坐标运算得出$\overrightarrow{a}•\overrightarrow{b}$的值,从而得到$f(x)=\frac{\sqrt{2}λ}{2}sin(2x-\frac{π}{4})+\frac{λ}{2}$,可以求出$2x-\frac{π}{4}∈[-π,\frac{π}{4}]$,讨论λ>0和λ<0两种情况,根据f(x)的最大值为$\frac{1}{2}$便可建立关于λ的方程,从而便可求出λ的值.
解答 解:(Ⅰ)$x=\frac{π}{3}$时,$\overrightarrow{a}=(\frac{\sqrt{3}}{2},\frac{1}{2})$;
∴$cos<\overrightarrow{a},\overrightarrow{c}>=\frac{\overrightarrow{a}•\overrightarrow{c}}{|\overrightarrow{a}||\overrightarrow{c}|}=\frac{-\frac{\sqrt{3}}{2}}{1•1}=-\frac{\sqrt{3}}{2}$;
∴$<\overrightarrow{a},\overrightarrow{c}>=\frac{5π}{6}$;
即向量$\overrightarrow{a},\overrightarrow{c}$的夹角为$\frac{5π}{6}$;
(Ⅱ)$\overrightarrow{a}•\overrightarrow{b}=si{n}^{2}x+sinxcosx=\frac{1-cos2x}{2}+\frac{1}{2}sin2x$=$\frac{\sqrt{2}}{2}sin(2x-\frac{π}{4})+\frac{1}{2}$;
∴$f(x)=\frac{\sqrt{2}λ}{2}sin(2x-\frac{π}{4})+\frac{λ}{2}$;
∵$x∈[-\frac{3π}{8},\frac{π}{4}]$;
∴$2x-\frac{π}{4}∈[-π,\frac{π}{4}]$;
①若λ<0,则$2x-\frac{π}{4}=-\frac{π}{2}$时,f(x)取最大值$-\frac{\sqrt{2}λ}{2}+\frac{λ}{2}=\frac{1}{2}$;
∴$λ=-1-\sqrt{2}$;
②若λ>0,则$2x-\frac{π}{4}=\frac{π}{4}$时,f(x)取最大值$\frac{\sqrt{2}λ}{2}•\frac{\sqrt{2}}{2}+\frac{λ}{2}=\frac{1}{2}$;
∴$λ=\frac{1}{2}$.
点评 考查向量夹角余弦的坐标公式,已知三角函数值求角,向量数量积的坐标运算,二倍角的正余弦公式,以及正弦函数在闭区间上的最值.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
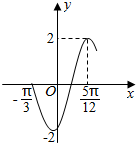
| A. | 函数f(x)的最小正周期是2π | |
| B. | 函数f(x)的图象可由函数g(x)=2sin2x的图象向右平移$\frac{π}{3}$个单位长度得到 | |
| C. | 函数f(x)的图象关于直线x=-$\frac{π}{12}$对称 | |
| D. | 函数f(x)在区间[-$\frac{7π}{12}$+kπ,-$\frac{π}{12}$+kπ](k∈Z)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+(y+2)2=3 | B. | (x-1)2+(y+2)2=9 | C. | (x-1)2+(y-2)2=4 | D. | (x-1)2+(y-2)2=12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com