
分析 可设剪成2段中的其中一段长为xcm,则其围成矩形后的长、宽分别为$\frac{2x}{6}$,$\frac{x}{6}$;另一段长为(l-x)cm,则其围成矩形后的长、宽分别为$\frac{3(l-x)}{10}$,$\frac{2(l-x)}{10}$,依题意可得两矩形的面积之和,再利用函数的导数,求函数的极小值,且为最小值即可.
解答 解:设剪成2段中其中一段为xcm,另一段为(l-x)cm,
依题意知:S=S1+S2=$\frac{x}{6}$•$\frac{x}{3}$+$\frac{3(l-x)}{10}$•$\frac{l-x}{5}$
=$\frac{1}{18}$x2+$\frac{3}{50}$(l-x)2,0<x<l,
可得S′=$\frac{1}{9}$x-$\frac{3}{25}$(l-x),
令S′=0,则x=$\frac{27}{52}$l,
当$\frac{27}{52}$l<x<l时,S′>0,函数s递增;
当0<x<$\frac{27}{52}$l,S′<0,函数s递减.
则函数s在x=$\frac{27}{52}$l处取得极小值,且为最小值$\frac{3}{104}{l^2}$.
故答案为:$\frac{3}{104}{l^2}$.
点评 本题考查函数的最值的求法,注意运用导数求函数的单调区间,可得函数的极值,且为最值,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | y平均增加3.5个单位 | B. | y平均增加2个单位 | ||
| C. | y平均减少3.5个单位 | D. | y平均减少2个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
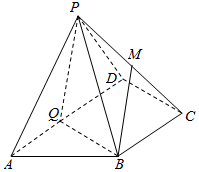 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ADC=90°,AD∥BC,平面PAD⊥底面ABCD,BC=$\frac{1}{2}$AD,PA=PD=AB=2,M,Q为AD,PC的中点
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ADC=90°,AD∥BC,平面PAD⊥底面ABCD,BC=$\frac{1}{2}$AD,PA=PD=AB=2,M,Q为AD,PC的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 4 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com