
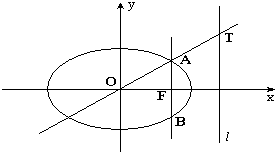
 如图,在平面直角坐标系xOy中.椭圆C:$\frac{x^2}{2}$+y2=1的右焦点为F,直线为l:x=2
如图,在平面直角坐标系xOy中.椭圆C:$\frac{x^2}{2}$+y2=1的右焦点为F,直线为l:x=2分析 (1)设G(x,y),由点G到点F和直线l的距离相等,列出方程,能求出点G的轨迹方程.
(2)由题意得xA=xF=c=1,将xA=1代入$\frac{{x}^{2}}{2}+{y}^{2}$=1,能求出AB.
(3)假设存在实数λ满足题意,由已知得OM:$y=\frac{{y}_{0}}{{x}_{0}}x$,$\frac{{x}_{0}x}{2}+{y}_{0}y=1$,椭圆C:$\frac{{x}^{2}}{2}+{y}^{2}=1$,分别联立方程组,能推导出存在实数λ=1,使得${\overrightarrow{OP}^2}=λ\overrightarrow{OM}•\overrightarrow{ON}$.
解答 解:(1)∵椭圆C:$\frac{x^2}{2}$+y2=1的右焦点为F,直线为l:x=2,∴F(1,0),
设G(x,y),∵点G到点F和直线l的距离相等,
∴$\sqrt{(x-1)^{2}+{y}^{2}}$=|x-2|,
整理,得y2=-2x+3.
∴点G的轨迹方程为y2=-2x+3.
(2)∵过点F作直线交椭圆C于点A,B,又直线OA交l于点T,$\overrightarrow{OT}=2\overrightarrow{OA}$,
∴AB⊥x轴,由题意得xA=xF=c=1,
∴将xA=1代入$\frac{{x}^{2}}{2}+{y}^{2}$=1,解得|yA|=$\frac{\sqrt{2}}{2}$,
∴AB=$\sqrt{2}$.
(3)假设存在实数λ满足题意,
由已知得OM:$y=\frac{{y}_{0}}{{x}_{0}}x$,①,$\frac{{x}_{0}x}{2}+{y}_{0}y=1$,②,椭圆C:$\frac{{x}^{2}}{2}+{y}^{2}=1$,③
由①②,得${x}_{N}=\frac{2{x}_{0}}{{{x}_{0}}^{2}+2{{y}_{0}}^{2}}$,${y}_{N}=\frac{2{y}_{0}}{{{x}_{0}}^{2}+2{{y}_{0}}^{2}}$,
由①③,得${{x}_{P}}^{2}=\frac{2{{x}_{0}}^{2}}{{{x}_{0}}^{2}+2{{y}_{0}}^{2}}$,${{y}_{P}}^{2}=\frac{2{{y}_{0}}^{2}}{{{x}_{0}}^{2}+2{{y}_{0}}^{2}}$,
∴${\overrightarrow{OP}}^{2}={{x}_{P}}^{2}+{{y}_{P}}^{2}$=$\frac{2{{x}_{0}}^{2}}{{{x}_{0}}^{2}+2{{y}_{0}}^{2}}+\frac{2{{y}_{0}}^{2}}{{{x}_{0}}^{2}+2{{y}_{0}}^{2}}$=$\frac{2({{x}_{0}}^{2}+{{y}_{0}}^{2})}{{{x}_{0}}^{2}+2{{y}_{0}}^{2}}$,
$\overrightarrow{OM}•\overrightarrow{ON}$=x0xN+y0yN=$\frac{2{{x}_{0}}^{2}}{{{x}_{0}}^{2}+2{{y}_{0}}^{2}}+\frac{2{{y}_{0}}^{2}}{{{x}_{0}}^{2}+2{{y}_{0}}^{2}}$=$\frac{2({{x}_{0}}^{2}+{{y}_{0}}^{2})}{{{x}_{0}}^{2}+2{{y}_{0}}^{2}}$.
∴存在实数λ=1,使得${\overrightarrow{OP}^2}=λ\overrightarrow{OM}•\overrightarrow{ON}$.
点评 本题考查点的轨迹方程的求法,考查线段长的求法,考查满足条件的实数是否存在的判断与求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<2} | B. | {x|1<x<2} | C. | {x|1≤x<2} | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X1 | 5 | 6 | 7 | 8 |
| P | 0.4 | a | b | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com