
| X1 | 5 | 6 | 7 | 8 |
| P | 0.4 | a | b | 0.1 |
·ÖÎö £¨1£©ÓÉEX1=6ºÍX1µÄ¸ÅÂÊ·Ö²¼ÁĐ£¬ÁĐ³ö·½³̀×飬ÄÜÇó³öa£¬bµÄÖµ£®
£¨2£©ÓÉ̉ÑÖªÇó³öÑù±¾µÄƵÂÊ·Ö²¼ÁĐºÍµÈ¼¶ÏµÊưX2µÄ¸ÅÂÊ·Ö²¼ÁĐ£¬´Ó¶øÄÜÇó³ö̉̉³§²úÆ·µÄµÈ¼¶ÏµÊưµÄÊưѧÆÚÍû£®
£¨3£©·Ö±đÇó³ö¼×³§ºÍ̉̉³§µÄĐԼ۱ȣ¬´Ó¶øµĂµ½̉̉³§µÄ²úÆ·¸ü¾ß¿É¹ºẬĐÔ£®
½â´đ ±¾̀âÂú·Ö£¨12·Ö£©
½â£º£¨1£©¡ßEX1=6£¬¡à5¡Á0.4+6a+7b+8¡Á0.1=6£¬
¼´6a+7b=3.2£¬
ÓÖÓÉX1µÄ¸ÅÂÊ·Ö²¼ÁеĂ0.4+a+b+0.1=1£¬¼´a+b=0.5£¬
ÓÉ$\left\{\begin{array}{l}{6a+7b=3.2}\\{a+b=0.5}\end{array}\right.$£¬½âµĂa=0.3£¬b=0.2£®£¨4·Ö£©
£¨2£©ÓÉ̉ÑÖªµĂ£¬Ñù±¾µÄƵÂÊ·Ö²¼ÁĐÈçÏ£º
| X2 | 3 | 4 | 5 | 6 | 7 | 8 |
| f | 0.3 | 0.2 | 0.2 | 0.1 | 0.1 | 0.1 |
| X2 | 3 | 4 | 5 | 6 | 7 | 8 |
| P | 0.3 | 0.2 | 0.2 | 0.1 | 0.1 | 0.1 |
µăÆÀ ±¾̀⿼²éÀëÉ¢ĐÍËæ»ú±äÁ¿µÄ·Ö²¼ÁĐ¡¢ÊưѧÆÚÍûµÄĐÔÖʵÄÓ¦ÓĂ£¬¿¼²éÊư¾ƯµÄ·Ö²¼¼°ƠûÀíÄÜÁ¦£¬ÊÇÖеµ̀⣮



| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | µÚ̉»ÏóÏ̃ | B£® | µÚ¶₫ÏóÏ̃ | C£® | µÚÈưÏóÏ̃ | D£® | µÚËÄÏóÏ̃ |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
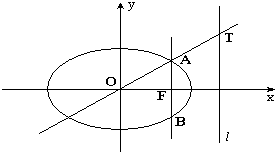 Èçͼ£¬ÔÚƽĂæÖ±½Ç×ø±êϵxOyÖĐ£®ÍÖÔ²C£º$\frac{x^2}{2}$+y2=1µÄÓ̉½¹µăΪF£¬Ö±ÏßΪl£ºx=2
Èçͼ£¬ÔÚƽĂæÖ±½Ç×ø±êϵxOyÖĐ£®ÍÖÔ²C£º$\frac{x^2}{2}$+y2=1µÄÓ̉½¹µăΪF£¬Ö±ÏßΪl£ºx=2²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | ?x0¡ÊN£¬x02¡Ư1 | B£® | ?x0¡ÊN£¬x02£¾1 | C£® | ?x¡ÊN£¬x2£¾1 | D£® | ?x¡ÊN£¬x2¡Ư1 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com