
���� �����������л�������Ǻ�����ͼ������ʼ�������f��x���Ľ���ʽ����һ�����ͼ��ĶԳ����ģ����ɵõ��յ�ֵ��
��������֪��������õ�sinC��ֵ�����C=$\frac{5��}{6}$����$g��B��=2sin��2B+\frac{��}{3}��$����$0��B��\frac{��}{6}$���õ�$\frac{��}{3}��2B+\frac{��}{3}��\frac{2��}{3}$���������g��B����ȡֵ��Χ��
��� �⣺����f��x��=$\overrightarrow a$•$\overrightarrow b$-1=$2si{n}^{2}��\frac{��}{4}+x��-\sqrt{3}cos2x-1$=2$sin��2x-\frac{��}{3}��$��
��$g��x��=f��x+ϕ��=2sin��2x+2ϕ-\frac{��}{3}��$��
��g��x����ͼ��ĶԳ�����Ϊ$��-ϕ+\frac{k��}{2}+\frac{��}{6}��0����k��Z$��
����֪�㣨$-\frac{��}{6}��0$��Ϊg��x����ͼ���һ���Գ����ģ���$ϕ=\frac{k��}{2}+\frac{��}{3}_{\;}^{\;}��k��Z��$��
��$ϕ�ʣ�0��\frac{��}{2}��$����$ϕ=\frac{��}{3}$��
������$sinC+cosC=1-\sqrt{2}sin\frac{C}{2}$��$2sin\frac{C}{2}cos\frac{C}{2}+1-2{sin^2}\frac{C}{2}=1-\sqrt{2}sin\frac{C}{2}$��
��$sin\frac{C}{2}��2cos\frac{C}{2}-2sin\frac{C}{2}+\sqrt{2}��=0$��
��$sin\frac{C}{2}��0$��
��$sin\frac{C}{2}-cos\frac{C}{2}=\frac{{\sqrt{2}}}{2}$��
����ƽ����$sinC=\frac{1}{2}$��
��$sin\frac{C}{2}-cos\frac{C}{2}=\frac{{\sqrt{2}}}{2}$��
��$sin\frac{C}{2}��cos\frac{C}{2}$����$\frac{��}{4}��\frac{C}{2}��\frac{��}{2}$��
��$\frac{��}{2}��C����$��$C=\frac{5��}{6}$��
��$g��B��=2sin��2B+\frac{��}{3}��$��
�֡�$0��B��\frac{��}{6}$����$\frac{��}{3}��2B+\frac{��}{3}��\frac{2��}{3}$��
��$g��B���ʣ�\sqrt{3}��2]$��
���� ������Ҫ�������Ǻ����еĺ�ȱ任Ӧ�ã����������Һ�����ͼ������ʣ��������Ǻ�����ʽ���������л����ǽ������Ĺؼ������е��⣮


 �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д� С����ȫ�ܼ��ϵ�д�
С����ȫ�ܼ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
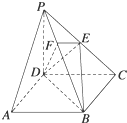 ��ͼ��ʾ��������P-ABCD�У�����ABCD�DZ߳�Ϊ2�������Σ�����PD�͵���ABCD��PD=DC��E��PC���е㣬��E����EF��PB��PB�ڵ�F����֤��
��ͼ��ʾ��������P-ABCD�У�����ABCD�DZ߳�Ϊ2�������Σ�����PD�͵���ABCD��PD=DC��E��PC���е㣬��E����EF��PB��PB�ڵ�F����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | -5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
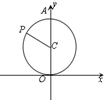 ��ͼ��ԲC��x2+��y-1��2=1��y����Ͻ���ΪA������P��A�������ԲC����ʱ�뷽���˶�������ת�ĽǶȡ�ACP=x��0��x��2�У�������$\overrightarrow{OP}$��$\overrightarrow a$=��0��1���������ӰΪy��OΪ����ԭ�㣩����y����x�ĺ���y=f��x����ͼ���ǣ�������
��ͼ��ԲC��x2+��y-1��2=1��y����Ͻ���ΪA������P��A�������ԲC����ʱ�뷽���˶�������ת�ĽǶȡ�ACP=x��0��x��2�У�������$\overrightarrow{OP}$��$\overrightarrow a$=��0��1���������ӰΪy��OΪ����ԭ�㣩����y����x�ĺ���y=f��x����ͼ���ǣ�������| A�� | 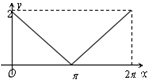 | B�� | 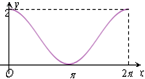 | C�� | 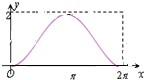 | D�� | 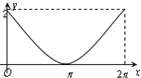 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| X1 | 5 | 6 | 7 | 8 |
| P | 0.4 | a | b | 0.1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 3-$\sqrt{3}$ | C�� | 2 | D�� | 3+$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com