
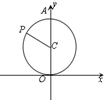
 如图,圆C:x2+(y-1)2=1与y轴的上交点为A,动点P从A点出发沿圆C按逆时针方向运动,设旋转的角度∠ACP=x(0≤x≤2π),向量$\overrightarrow{OP}$在$\overrightarrow a$=(0,1)方向的射影为y(O为坐标原点),则y关于x的函数y=f(x)的图象是( )
如图,圆C:x2+(y-1)2=1与y轴的上交点为A,动点P从A点出发沿圆C按逆时针方向运动,设旋转的角度∠ACP=x(0≤x≤2π),向量$\overrightarrow{OP}$在$\overrightarrow a$=(0,1)方向的射影为y(O为坐标原点),则y关于x的函数y=f(x)的图象是( )| A. | 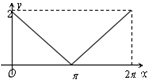 | B. | 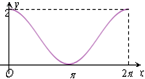 | C. | 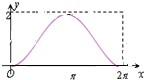 | D. | 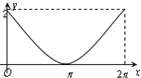 |
分析 求出$\overrightarrow{OP}$的坐标,代入向量的投影公式得出y关于x的函数即可判断.
解答 解:∵∠ACP=x,∴P(-sinx,1+cosx),
∴$\overrightarrow{OP}$=(-sinx,1+cosx),
∴y=|$\overrightarrow{OP}$|•$\frac{\overrightarrow{OP}•\overrightarrow{a}}{|\overrightarrow{OP}||\overrightarrow{a}|}$=$\frac{1+cosx}{1}$=1+cosx,
故选B.
点评 本题考查了函数解析式的求解,向量的数量积运算,属于中档题.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题p∧q是真命题 | B. | 命题p∧¬q是真命题 | ||
| C. | 命题¬p∧q是真命题 | D. | 命题¬p∨¬q是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在回归分析中,变量间的关系若是非确定性关系,那么因变量不能由自变量唯一确定 | |
| B. | 线性相关系数可以是正的也可以是负的 | |
| C. | 在回归分析中,如果r2=1或r=±1,说明x与y之间完全线性相关 | |
| D. | 样本相关系数r∈(-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈N,x02≥1 | B. | ?x0∈N,x02>1 | C. | ?x∈N,x2>1 | D. | ?x∈N,x2≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{5}+\frac{2}{5}i$ | B. | $-\frac{1}{5}-\frac{2}{5}i$ | C. | $\frac{1}{5}+\frac{2}{5}i$ | D. | $\frac{1}{5}-\frac{2}{5}i$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com