
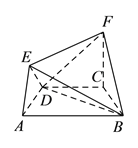
【题目】在如图所示的几何体中,四边形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
(![]() )在线段
)在线段![]() (含端点)上,是否存在一点
(含端点)上,是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(![]() )见解析;(
)见解析;(![]() )
)![]() ;(
;(![]() )存在,
)存在, ![]()
【解析】试题分析:(1)由题意,证明![]() ,
, ![]() ,证明
,证明![]() 面
面![]() ;(2)建立空间直角坐标系,求平面
;(2)建立空间直角坐标系,求平面![]() 和平面
和平面![]() 的法向量,解得余弦值为
的法向量,解得余弦值为![]() ;(3)得
;(3)得![]() ,
, 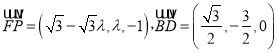 ,所以
,所以![]() ,
, ![]() ,所以存在
,所以存在![]() 为
为![]() 中点.
中点.
试题解析:
(![]() )∵
)∵![]() ,
, ![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
, ![]() .
.
∵![]() ,且
,且![]() ,
,
![]() 、
、![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
(![]() )知
)知![]() ,∴
,∴![]() .
.
∵![]() 面
面![]() ,
, ![]() ,
, ![]() ,
, ![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,
为坐标原点,
以![]() ,
, ![]() ,
, ![]() 为
为![]() ,
, ![]() ,
, ![]() 轴建系.
轴建系.
设![]() ,则
,则![]() ,
, ![]() ,
,  ,
, ![]() ,
, ![]() ,
,
∴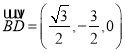 ,
, ![]() .
.
设![]() 的一个法向量为
的一个法向量为![]() ,
,
∴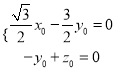 ,取
,取![]() ,则
,则![]() .
.
由于![]() 是面
是面![]() 的法向量,
的法向量,
则 .
.
∵二面角![]() 为锐二面角,∴余弦值为
为锐二面角,∴余弦值为![]() .
.
(![]() )存在点
)存在点![]() .
.
设![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() .
.
∵![]() 面
面![]() ,
,  .
.
若![]() 面
面![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴存在
,∴存在![]() 为
为![]() 中点.
中点.

【题型】解答题
【结束】
19
【题目】已知函数![]() .
.
(![]() )当
)当![]() 时,求此函数对应的曲线在
时,求此函数对应的曲线在![]() 处的切线方程.
处的切线方程.
(![]() )求函数
)求函数![]() 的单调区间.
的单调区间.
(![]() )对
)对![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() .过
.过![]() 的平面交
的平面交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
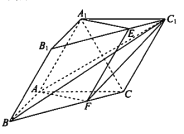
(l)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)记四棱锥![]() 的体积为
的体积为![]() ,三棱柱
,三棱柱![]() 的体积为
的体积为![]() .若
.若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() = (1,2sinθ),
= (1,2sinθ),![]() = (sin(θ+
= (sin(θ+![]() ),1),θ
),1),θ![]() R。
R。
(1) 若![]() ⊥
⊥![]() ,求 tanθ的值;
,求 tanθ的值;
(2) 若![]() ∥
∥![]() ,且 θ
,且 θ![]() (0,
(0,![]() ),求 θ的值
),求 θ的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个空间图形,使B、C、D三点重合,重合后的点记为H,那么,在这个空间图形中必有( )
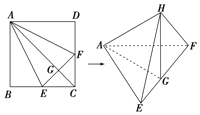
A. ![]() 所在平面B.
所在平面B. ![]() 所在平面
所在平面
C. ![]() 所在平面D.
所在平面D. ![]() 所在平面
所在平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为3的正方形,
是边长为3的正方形, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)在![]() 上是否存在一点
上是否存在一点![]() ,使平面
,使平面![]() 将几何体
将几何体![]() 分成上下两部分的体积比为
分成上下两部分的体积比为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于古典概型的说法中正确的是( )
①试验中所有可能出现的基本事件只有有限个;
②每个事件出现的可能性相等;
③每个基本事件出现的可能性相等;
④基本事件的总数为n,随机事件A若包含k个基本事件,则![]() .
.
A. ②④ B. ③④ C. ①④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com