
【题目】写出与α=-1910°终边相同的角的集合,并把集合中适合不等式-720°≤β<360°的元素β写出来.
【答案】{β|β=k·360°-1 910°,k∈Z};元素β见解析
【解析】
把α=-1 910°加上![]() 可得与α=-1 910°终边相同的角的集合,分别取k=4,5,6,求得适合不等式-720°≤β<360°的元素β.
可得与α=-1 910°终边相同的角的集合,分别取k=4,5,6,求得适合不等式-720°≤β<360°的元素β.
与α=-1 910°终边相同的角的集合为{β|β=k·360°-1910°,k∈Z}.
∵-720°≤β<360°,即-720°≤k·360°-1 910°<360°(k∈Z),∴![]() (k∈Z),故取k=4,5,6.
(k∈Z),故取k=4,5,6.
k=4时,β=4×360°-1910°=-470°;
k=5时,β=5×360°-1910°=-110°;
k=6时,β=6×360°-1910°=250°.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某次文艺汇演,要将A、B、C、D、E、F这六个不同节目编排成节目单,如下表:

如果A、B两个节目要相邻,且都不排在第3号位置,则节目单上不同的排序方式有( )种
A. 192 B. 144 C. 96 D. 72
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月,来自“一带一路”沿线的![]() 国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.为发展业务,某调研组对
国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.为发展业务,某调研组对![]() 两个公司的扫码支付准备从国内
两个公司的扫码支付准备从国内![]() 个人口超过
个人口超过![]() 万的超大城市和
万的超大城市和![]() 个人口低于
个人口低于![]() 万的小城市随机抽取若干个进行统计,若一次抽取
万的小城市随机抽取若干个进行统计,若一次抽取![]() 个城市,全是小城市的概率为
个城市,全是小城市的概率为![]() .
.
(I)求![]() 的值;
的值;
(Ⅱ)若一次抽取![]() 个城市,则:
个城市,则:
①假设取出小城市的个数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
②取出![]() 个城市是同一类城市求全为超大城市的概率.
个城市是同一类城市求全为超大城市的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】峰谷电是目前在城市居民当中开展的一种电价类别.它是将一天24小时划分成两个时间段,把8:00—22:00共14小时称为峰段,执行峰电价,即电价上调;22:00—次日8:00共10个小时称为谷段,执行谷电价,即电价下调.为了进一步了解民众对峰谷电价的使用情况,从某市一小区随机抽取了50 户住户进行夏季用电情况调查,各户月平均用电量以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:度)分组的频率分布直方图如下图:
(单位:度)分组的频率分布直方图如下图:

若将小区月平均用电量不低于700度的住户称为“大用户”,月平均用电量低于700度的住户称为“一般用户”.其中,使用峰谷电价的户数如下表:
月平均用电量(度) |
|
|
|
|
|
|
使用峰谷电价的户数 | 3 | 9 | 13 | 7 | 2 | 1 |
(1)估计所抽取的 50户的月均用电量的众数和平均数(同一组中的数据用该组区间的中点值作代表);
(2)(![]() )将“一般用户”和“大用户”的户数填入下面
)将“一般用户”和“大用户”的户数填入下面![]() 的列联表:
的列联表:
一般用户 | 大用户 | |
使用峰谷电价的用户 | ||
不使用峰谷电价的用户 |
(![]() )根据(
)根据(![]() )中的列联表,能否有
)中的列联表,能否有![]() 的把握认为 “用电量的高低”与“使用峰谷电价”有关?
的把握认为 “用电量的高低”与“使用峰谷电价”有关?
| 0.025 | 0.010 | 0.001 |
| 5.024 | 6.635 | 10.828 |
附:![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
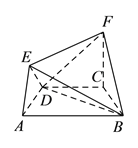
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
(![]() )在线段
)在线段![]() (含端点)上,是否存在一点
(含端点)上,是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(![]() )见解析;(
)见解析;(![]() )
)![]() ;(
;(![]() )存在,
)存在, ![]()
【解析】试题分析:(1)由题意,证明![]() ,
, ![]() ,证明
,证明![]() 面
面![]() ;(2)建立空间直角坐标系,求平面
;(2)建立空间直角坐标系,求平面![]() 和平面
和平面![]() 的法向量,解得余弦值为
的法向量,解得余弦值为![]() ;(3)得
;(3)得![]() ,
, 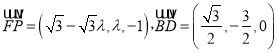 ,所以
,所以![]() ,
, ![]() ,所以存在
,所以存在![]() 为
为![]() 中点.
中点.
试题解析:
(![]() )∵
)∵![]() ,
, ![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
, ![]() .
.
∵![]() ,且
,且![]() ,
,
![]() 、
、![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
(![]() )知
)知![]() ,∴
,∴![]() .
.
∵![]() 面
面![]() ,
, ![]() ,
, ![]() ,
, ![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,
为坐标原点,
以![]() ,
, ![]() ,
, ![]() 为
为![]() ,
, ![]() ,
, ![]() 轴建系.
轴建系.
设![]() ,则
,则![]() ,
, ![]() ,
,  ,
, ![]() ,
, ![]() ,
,
∴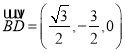 ,
, ![]() .
.
设![]() 的一个法向量为
的一个法向量为![]() ,
,
∴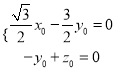 ,取
,取![]() ,则
,则![]() .
.
由于![]() 是面
是面![]() 的法向量,
的法向量,
则 .
.
∵二面角![]() 为锐二面角,∴余弦值为
为锐二面角,∴余弦值为![]() .
.
(![]() )存在点
)存在点![]() .
.
设![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() .
.
∵![]() 面
面![]() ,
, 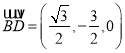 .
.
若![]() 面
面![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴存在
,∴存在![]() 为
为![]() 中点.
中点.

【题型】解答题
【结束】
19
【题目】已知函数![]() .
.
(![]() )当
)当![]() 时,求此函数对应的曲线在
时,求此函数对应的曲线在![]() 处的切线方程.
处的切线方程.
(![]() )求函数
)求函数![]() 的单调区间.
的单调区间.
(![]() )对
)对![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com