
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,过焦点
上,过焦点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点.
两点.
(1)求抛物线![]() 的方程以及
的方程以及![]() 的值;
的值;
(2)记抛物线![]() 的准线与
的准线与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)y2=4x,2(2)![]()
【解析】
(1)依题意,![]() ,即可求的抛物线方程,再根据抛物线的定义,直接可以写出
,即可求的抛物线方程,再根据抛物线的定义,直接可以写出![]() 的值.
的值.
(2)设l:x=my+1,M(x1,y1)、N(x2,y2),联立方程,消去x,得关于y的一元二次方程,由![]() ,得
,得![]() ,再根据
,再根据![]() ,求得m的值,即可求得
,求得m的值,即可求得![]() 的值.
的值.
解:(1)![]() 抛物线
抛物线![]() 的焦点
的焦点![]()
![]() ,
,
![]()
![]() ,则
,则![]() ,抛物线方程为
,抛物线方程为![]() ;
;
![]() 点
点![]() 在抛物线
在抛物线![]() 上
上
![]()
![]() .
.
(2)依题意,F(1,0),设l:x=my+1,设M(x1,y1)、N(x2,y2),
联立方程![]() ,消去x,得y2﹣4my﹣4=0.
,消去x,得y2﹣4my﹣4=0.
所以![]() ,① 且
,① 且![]() ,
,
又![]() ,则(1﹣x1,﹣y1)=λ(x2﹣1,y2),即y1=﹣λy2,
,则(1﹣x1,﹣y1)=λ(x2﹣1,y2),即y1=﹣λy2,
代入①得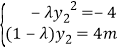 ,消去y2得
,消去y2得![]() ,
,
B(﹣1,0),则![]() ,
,
则![]()
![]()
![]()
![]()
![]() (m2+1)(16m2+8)+4m4m+8=16m4+40m2+16,
(m2+1)(16m2+8)+4m4m+8=16m4+40m2+16,
当16m4+40m2+16=40,解得![]() ,故
,故![]() .
.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若函数![]() 在
在![]() 处取得极值,求实数
处取得极值,求实数![]() 的值;
的值;
(2)在(1)的结论下,若关于![]() 的不等式
的不等式![]() ,当
,当![]() 时恒成立,求
时恒成立,求![]() 的值;
的值;
(3)令![]() ,若关于
,若关于![]() 的方程
的方程![]() 在
在![]() 内至少有两个解,求出实数
内至少有两个解,求出实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》第八章“方程”问题八:今有卖牛二、羊五,以买十三豕,有余钱一千。卖牛三、豕三,以买九羊,钱适足.卖羊六、豕八,以买五牛,钱不足六百.问牛、羊、豕各几何?“如果卖掉2头牛和5只羊,可买13口猪,还余1000钱;卖掉3头牛和3口猪的钱恰好可买9只羊;而卖掉6只羊和8口猪,去买5头牛,还少600钱.问牛、羊、猪的价格各是多少”.按照题意,可解出牛______钱、羊______钱、猪______钱.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次文艺汇演,要将A、B、C、D、E、F这六个不同节目编排成节目单,如下表:

如果A、B两个节目要相邻,且都不排在第3号位置,则节目单上不同的排序方式有( )种
A. 192 B. 144 C. 96 D. 72
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,
时,
①若曲线![]() 与直线
与直线![]() 相切,求c的值;
相切,求c的值;
②若曲线![]() 与直线
与直线![]() 有公共点,求c的取值范围.
有公共点,求c的取值范围.
(2)当![]() 时,不等式
时,不等式![]() 对于任意正实数x恒成立,当c取得最大值时,求a,b的值.
对于任意正实数x恒成立,当c取得最大值时,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月,来自“一带一路”沿线的![]() 国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.为发展业务,某调研组对
国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.为发展业务,某调研组对![]() 两个公司的扫码支付准备从国内
两个公司的扫码支付准备从国内![]() 个人口超过
个人口超过![]() 万的超大城市和
万的超大城市和![]() 个人口低于
个人口低于![]() 万的小城市随机抽取若干个进行统计,若一次抽取
万的小城市随机抽取若干个进行统计,若一次抽取![]() 个城市,全是小城市的概率为
个城市,全是小城市的概率为![]() .
.
(I)求![]() 的值;
的值;
(Ⅱ)若一次抽取![]() 个城市,则:
个城市,则:
①假设取出小城市的个数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
②取出![]() 个城市是同一类城市求全为超大城市的概率.
个城市是同一类城市求全为超大城市的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
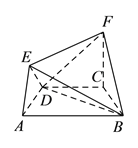
【题目】在如图所示的几何体中,四边形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
(![]() )在线段
)在线段![]() (含端点)上,是否存在一点
(含端点)上,是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(![]() )见解析;(
)见解析;(![]() )
)![]() ;(
;(![]() )存在,
)存在, ![]()
【解析】试题分析:(1)由题意,证明![]() ,
, ![]() ,证明
,证明![]() 面
面![]() ;(2)建立空间直角坐标系,求平面
;(2)建立空间直角坐标系,求平面![]() 和平面
和平面![]() 的法向量,解得余弦值为
的法向量,解得余弦值为![]() ;(3)得
;(3)得![]() ,
, 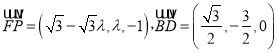 ,所以
,所以![]() ,
, ![]() ,所以存在
,所以存在![]() 为
为![]() 中点.
中点.
试题解析:
(![]() )∵
)∵![]() ,
, ![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
, ![]() .
.
∵![]() ,且
,且![]() ,
,
![]() 、
、![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
(![]() )知
)知![]() ,∴
,∴![]() .
.
∵![]() 面
面![]() ,
, ![]() ,
, ![]() ,
, ![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,
为坐标原点,
以![]() ,
, ![]() ,
, ![]() 为
为![]() ,
, ![]() ,
, ![]() 轴建系.
轴建系.
设![]() ,则
,则![]() ,
, ![]() ,
,  ,
, ![]() ,
, ![]() ,
,
∴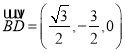 ,
, ![]() .
.
设![]() 的一个法向量为
的一个法向量为![]() ,
,
∴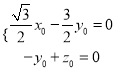 ,取
,取![]() ,则
,则![]() .
.
由于![]() 是面
是面![]() 的法向量,
的法向量,
则 .
.
∵二面角![]() 为锐二面角,∴余弦值为
为锐二面角,∴余弦值为![]() .
.
(![]() )存在点
)存在点![]() .
.
设![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() .
.
∵![]() 面
面![]() ,
, 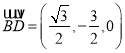 .
.
若![]() 面
面![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴存在
,∴存在![]() 为
为![]() 中点.
中点.

【题型】解答题
【结束】
19
【题目】已知函数![]() .
.
(![]() )当
)当![]() 时,求此函数对应的曲线在
时,求此函数对应的曲线在![]() 处的切线方程.
处的切线方程.
(![]() )求函数
)求函数![]() 的单调区间.
的单调区间.
(![]() )对
)对![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com