
分析 (Ⅰ)根据题意,1-x+x2-x3=$\frac{1{-(-x)}^{4}}{1-(-x)}$,利用放缩法得$\frac{1{-x}^{4}}{1+x}$≤$\frac{1}{1+x}$,即可证明结论成立;
(Ⅱ)利用0≤x≤1时x3≤x,证明f(x)≤$\frac{3}{2}$,再利用配方法证明f(x)≥$\frac{3}{4}$,结合函数的最小值得出f(x)>$\frac{3}{4}$,即证结论成立.
解答 解:(Ⅰ)证明:因为f(x)=x3+$\frac{1}{x+1}$,x∈[0,1],
且1-x+x2-x3=$\frac{1{-(-x)}^{4}}{1-(-x)}$=$\frac{1{-x}^{4}}{1+x}$,
所以$\frac{1{-x}^{4}}{1+x}$≤$\frac{1}{1+x}$,
所以1-x+x2-x3≤$\frac{1}{x+1}$,
即f(x)≥1-x+x2;
(Ⅱ)证明:因为0≤x≤1,所以x3≤x,
所以f(x)=x3+$\frac{1}{x+1}$≤x+$\frac{1}{x+1}$=x+$\frac{1}{x+1}$-$\frac{3}{2}$+$\frac{3}{2}$=$\frac{(x-1)(2x+1)}{2(x+1)}$+$\frac{3}{2}$≤$\frac{3}{2}$;
由(Ⅰ)得,f(x)≥1-x+x2=${(x-\frac{1}{2})}^{2}$+$\frac{3}{4}$≥$\frac{3}{4}$,
且f($\frac{1}{2}$)=${(\frac{1}{2})}^{3}$+$\frac{1}{1+\frac{1}{2}}$=$\frac{19}{24}$>$\frac{3}{4}$,
所以f(x)>$\frac{3}{4}$;
综上,$\frac{3}{4}$<f(x)≤$\frac{3}{2}$.
点评 本题主要考查了函数的单调性与最值,分段函数等基础知识,也考查了推理与论证,分析问题与解决问题的能力,是综合性题目.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {3,5} | C. | {1,2,4,6} | D. | {1,2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
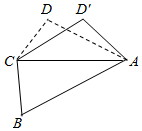 如图,已知平面四边形ABCD,AB=BC=3,CD=1,AD=$\sqrt{5}$,∠ADC=90°,沿直线AC将△ACD翻折成△ACD′,直线AC与BD′所成角的余弦的最大值是$\frac{\sqrt{6}}{6}$.
如图,已知平面四边形ABCD,AB=BC=3,CD=1,AD=$\sqrt{5}$,∠ADC=90°,沿直线AC将△ACD翻折成△ACD′,直线AC与BD′所成角的余弦的最大值是$\frac{\sqrt{6}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 6 | C. | -4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.90 | B. | 0.30 | C. | 0.60 | D. | 0.40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com