
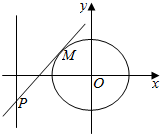
 已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.分析 (1)利用题设条件,根据焦点和椭圆的定义求得c和a,进而求得b,由此能求出椭圆的方程;
(2)设M的坐标,得到过点M的椭圆的切线方程,求出两种特殊情况的以PM为直径的圆所过的定点,然后证明一般情况下成立得答案.
解答 解:(1)∵中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点,
∴c=2,左焦点F′(-2,0),
∴2a=|AF|+|AF′|=$\sqrt{(2+2)^{2}+{3}^{2}}+\sqrt{(2-2)^{2}+{3}^{2}}=8$,
解得c=2,a=4,
又a2=b2+c2,
∴b2=12,
故椭圆C的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$;
(2)设M(x0,y0),
则椭圆过点M的切线方程为$\frac{{x}_{0}x}{16}+\frac{{y}_{0}y}{12}=1$,
取x=-8,得y=$\frac{6{x}_{0}+12}{{y}_{0}}$,
∴P(-8,$\frac{6{x}_{0}+12}{{y}_{0}}$),
当M为椭圆上顶点时,M(0,$2\sqrt{3}$),此时P(-8,$2\sqrt{3}$),
PM的中点为(-4,$2\sqrt{3}$),
则以PM为直径的圆的方程为$(x+4)^{2}+(y-2\sqrt{3})^{2}=16$,
取y=0,可得圆过定点G(-2,0),H(-6,0);
同理当M为椭圆下顶点时,可得以PM为直接的圆过定点G(-2,0),H(-6,0).
∵$\overrightarrow{MG}=(-2-{x}_{0},-{y}_{0})$,$\overrightarrow{PG}=(6,-\frac{6{x}_{0}+12}{{y}_{0}})$,
∴$\overrightarrow{MG}•\overrightarrow{PG}=-12-6{x}_{0}+6{x}_{0}+12=0$,
∴以PM为直径的圆过定点G(-2,0);
∵$\overrightarrow{MH}=(-6-{x}_{0},-{y}_{0})$,$\overrightarrow{PH}=(2,-\frac{6{x}_{0}+12}{{y}_{0}})$,
∴$\overrightarrow{MH}•\overrightarrow{PH}=-12-2{x}_{0}+6{x}_{0}+12=4{x}_{0}≠0$.
故以PM为直径的圆过定点G(-2,0).
点评 本题考查椭圆标准方程的求法,考查了过椭圆上点的切线方程,训练了恒过定点问题的求解方法,是中档题.


科目:高中数学 来源: 题型:解答题
 阅读如图所示程序框图,根据框图的算法功能回答下列问题:
阅读如图所示程序框图,根据框图的算法功能回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
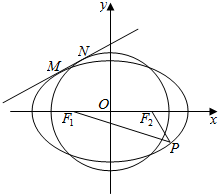 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,P为椭圆C上任意一点,当|PF1|-|PF2|取最大值时,|PF1|=3,|PF2|=1.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,P为椭圆C上任意一点,当|PF1|-|PF2|取最大值时,|PF1|=3,|PF2|=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com