
分析 (1)根据同角三角函数基本关系式消去参数,即可得到其普通方程;
(2)根据1+tan2θ=$\frac{1}{co{s}^{2}θ}$,消去参数,即可得到其普通方程;
(3)用代入法消去参数,得到所求的普通方程,然后,给出该方程对应的轨迹即可.
解答 解:(1)根据已知,得
$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
它表示一个焦点在x轴上的椭圆,
(2)结合1+tan2θ=$\frac{1}{co{s}^{2}θ}$,得
消去参数φ,得
1+$\frac{{y}^{2}}{{b}^{2}}$=$\frac{{x}^{2}}{{a}^{2}}$,
∴$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$,
它表示一个焦点在x轴上的双曲线,
(3)根据已知参数方程,消去参数,得
y2=2px,(p>0),
它表示一个焦点在x轴正半轴上的抛物线.
点评 本题综合考查了椭圆、双曲线、抛物线的参数方程和普通方程的互化、三角公式的应用等知识,考查比较综合,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 抛一枚硬币10次,一定有5次正面向上 | |
| B. | 明天本地降水概率为70%,是指本地下雨的面积是70% | |
| C. | 互斥事件一定是对立事件,对立事件不一定是互斥事件 | |
| D. | 若A与B为互斥事件,则P(A)+P(B)≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3+2$\sqrt{2}$ | B. | 4+2$\sqrt{3}$ | C. | 6+4$\sqrt{2}$ | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
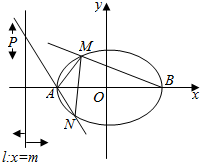 已知椭圆C的中心在原点,焦点在x轴上,离心率e=$\frac{\sqrt{3}}{2}$,短半轴长b=1.
已知椭圆C的中心在原点,焦点在x轴上,离心率e=$\frac{\sqrt{3}}{2}$,短半轴长b=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
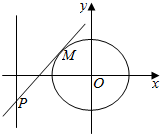 已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com