
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据逆否命题的定义进行判断.
②根据充分条件和必要条件的定义进行判断.
③根据复合命题真假关系进行判断.
④根据含有量词的命题的否定进行判断.
解答 解:①命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”;故①正确,
②由a2+a≠0得a≠-1或a≠0,“a≠0”是“a2+a≠0”的必要不充分条件;故②正确,
③若p∧q为假命题,则p,q质数有一个为假命题;故③错误,
④命题p:?x0∈R,使得x02+x0+1<0,则¬p:?x∈R,都有x2+x+1≥0.故④正确,
故正确的是①②④,
故选:C
点评 本题主要考查命题的真假判断,涉及四种命题的关系,充分条件和必要条件的判断以及复合命题,含有量词的命题的否定,综合性较强,难度不大.


 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
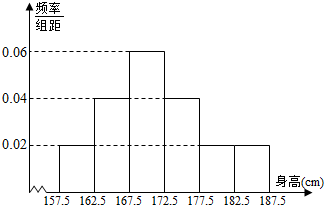
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
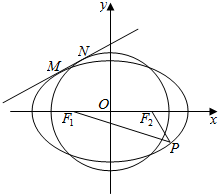 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,P为椭圆C上任意一点,当|PF1|-|PF2|取最大值时,|PF1|=3,|PF2|=1.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,P为椭圆C上任意一点,当|PF1|-|PF2|取最大值时,|PF1|=3,|PF2|=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
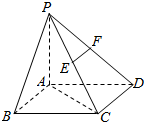 如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,E,F分别是PC,PD的中点,PA=$\sqrt{3}$AD=$\sqrt{3}$AB=$\sqrt{3}$.
如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,E,F分别是PC,PD的中点,PA=$\sqrt{3}$AD=$\sqrt{3}$AB=$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com