
分析 ①根据直线l、m的方向向量$\overrightarrow{a}$与$\overrightarrow{b}$垂直,得出l⊥m;
②根据直线l的方向向量$\overrightarrow{a}$与平面α的法向量$\overrightarrow{n}$垂直,不能判断l⊥α;
③根据平面α、β的法向量$\overrightarrow{{n}_{1}}$与$\overrightarrow{{n}_{2}}$不共线,不能得出α∥β;
④求出向量$\overrightarrow{AB}$与$\overrightarrow{BC}$的坐标表示,再利用平面α的法向量$\overrightarrow{n}$,列出方程组求出u+t的值.
解答 解:对于①,∵$\overrightarrow{a}$=(1,-1,2),$\overrightarrow{b}$=(2,1,-$\frac{1}{2}$),
∴$\overrightarrow{a}$•$\overrightarrow{b}$=1×2-1×1+2×(-$\frac{1}{2}$)=0,
∴$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴直线l与m垂直,①正确;
对于②,$\overrightarrow{a}$=(0,1,-1),$\overrightarrow{n}$=(1,-1,-1),
∴$\overrightarrow{a}$•$\overrightarrow{n}$=0×1+1×(-1)+(-1)×(-1)=0,
∴$\overrightarrow{a}$⊥$\overrightarrow{n}$,∴l∥α或l?α,②错误;
对于③,∵$\overrightarrow{{n}_{1}}$=(0,1,3),$\overrightarrow{{n}_{2}}$=(1,0,2),
∴$\overrightarrow{{n}_{1}}$与$\overrightarrow{{n}_{2}}$不共线,
∴α∥β不成立,③错误;
对于④,∵点A(1,0,-1),B(0,1,0),C(-1,2,0),
∴$\overrightarrow{AB}$=(-1,1,1),$\overrightarrow{BC}$=(-1,1,0),
向量$\overrightarrow{n}$=(1,u,t)是平面α的法向量,
∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=0}\\{\overrightarrow{n}•\overrightarrow{BC}=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{-1+u+t=0}\\{-1+u=0}\end{array}\right.$;
则u+t=1,④正确.
综上,以上真命题的序号是①④.
故答案为:①④.
点评 本题考查了空间向量的应用问题,也考查了直线的方向向量与平面的法向量的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
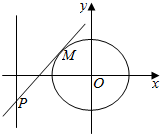 已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
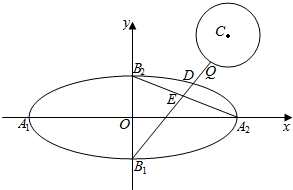 如图,已知椭圆$\frac{{x}^{2}}{2}$+y2=1的四个顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,若圆C:(x-3)2+(y-3)2=r2(0<r<3)上有且只有一个点P满足$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\sqrt{5}$.
如图,已知椭圆$\frac{{x}^{2}}{2}$+y2=1的四个顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,若圆C:(x-3)2+(y-3)2=r2(0<r<3)上有且只有一个点P满足$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
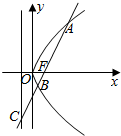 如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )
如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com