
分析 根据三角函数的倍角公式先求出a的值,利用余弦定理进行求解即可.
解答 解:在△ABC中,∵b=3,c=1,A=2B,
∴$\frac{b}{sinB}=\frac{a}{sinA}=\frac{a}{2sinBcosB}$,
即a=2bcosB=6cosB,
由余弦定理可知,cosB=$\frac{36co{s}^{2}B+1-9}{2×6cosB}$,
整理得cosB=$\frac{\sqrt{3}}{3}$,则a=6cosB=2$\sqrt{3}$,
则cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{12+9-1}{2×2\sqrt{3}×3}$=$\frac{20}{12\sqrt{3}}$=$\frac{5\sqrt{3}}{9}$,
故答案为:$\frac{5\sqrt{3}}{9}$
点评 本题主要考查解三角形的应用,利用正弦定理余弦定理以及三角函数的倍角公式进行化简是解决本题的关键.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
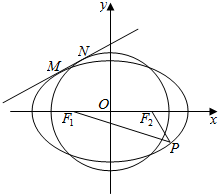 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,P为椭圆C上任意一点,当|PF1|-|PF2|取最大值时,|PF1|=3,|PF2|=1.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,P为椭圆C上任意一点,当|PF1|-|PF2|取最大值时,|PF1|=3,|PF2|=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-$\frac{\sqrt{3}π}{24}$ | B. | 1-$\frac{\sqrt{3}π}{12}$ | C. | $\frac{\sqrt{3}π}{24}$ | D. | $\frac{\sqrt{3}π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
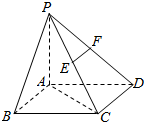 如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,E,F分别是PC,PD的中点,PA=$\sqrt{3}$AD=$\sqrt{3}$AB=$\sqrt{3}$.
如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,E,F分别是PC,PD的中点,PA=$\sqrt{3}$AD=$\sqrt{3}$AB=$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com