
分析 (1)由题意可得|2x+m|≤1,即$\frac{-1-m}{2}$≤x≤$\frac{1-m}{2}$,可得$\left\{\begin{array}{l}{-3≤\frac{1-m}{2}<-2}\\{-4<\frac{-1-m}{2}≤-3}\end{array}\right.$,解不等式即可得到所求整数m的值;
(2)由题意可得2|x-1|-a>-|x+3|,即为a<2|x-1|+|x+3|的最小值,由绝对值的含义和一次函数的单调性,即可得到最小值,进而得到a的范围.
解答 解:(1)关于x的不等式g(x)≥-1的整数解有且仅有一值为-3,
即为|2x+m|≤1,即$\frac{-1-m}{2}$≤x≤$\frac{1-m}{2}$,
可得$\left\{\begin{array}{l}{-3≤\frac{1-m}{2}<-2}\\{-4<\frac{-1-m}{2}≤-3}\end{array}\right.$,即为$\left\{\begin{array}{l}{5<m≤7}\\{5≤m<7}\end{array}\right.$,
即有5<m<7,可得整数m=6;
(2)函数y=f(x)的图象恒在函数y=$\frac{1}{2}$g(x)的上方,
即有2|x-1|-a>-|x+3|,
即为a<2|x-1|+|x+3|的最小值,
由y=2|x-1|+|x+3|=$\left\{\begin{array}{l}{3x+1,x≥1}\\{5-x,-3<x<1}\\{-3x-1,x≤-3}\end{array}\right.$,
可得x=1时,取得最小值4,
可得a的范围是(-∞,4).
点评 本题考查绝对值不等式的解法,考查不等式恒成立问题的解法,注意运用参数分离和绝对值的含义,以及一次函数的单调性,考查运算能力,属于中档题.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:解答题
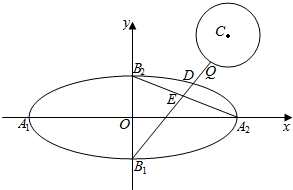 如图,已知椭圆$\frac{{x}^{2}}{2}$+y2=1的四个顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,若圆C:(x-3)2+(y-3)2=r2(0<r<3)上有且只有一个点P满足$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\sqrt{5}$.
如图,已知椭圆$\frac{{x}^{2}}{2}$+y2=1的四个顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,若圆C:(x-3)2+(y-3)2=r2(0<r<3)上有且只有一个点P满足$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5x-5y-4=0 | B. | 5x-5y+4=0. | C. | 5x+5y-4=0 | D. | 3x+5y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com