
| A. | 1-$\frac{\sqrt{3}π}{24}$ | B. | 1-$\frac{\sqrt{3}π}{12}$ | C. | $\frac{\sqrt{3}π}{24}$ | D. | $\frac{\sqrt{3}π}{12}$ |
分析 根据几何概型的概率公式求出对应区域的面积进行求解即可.
解答 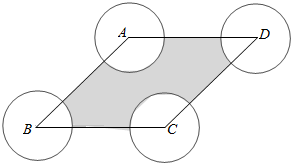 解:分别以A,B,C,D为圆心,1为半径的圆,
解:分别以A,B,C,D为圆心,1为半径的圆,
则所以概率对应的面积为阴影部分,
则四个圆在菱形内的扇形夹角之和为2π,
则对应的四个扇形之和的面积为一个整圆的面积S=π×12=π,
∵S菱形ABCD=AB•BCsin$\frac{π}{3}$=4×4×$\frac{\sqrt{3}}{2}$=8$\sqrt{3}$,
∴S阴影=S菱形ABCD-S空白=8$\sqrt{3}$-π×12=8$\sqrt{3}$-π.
因此,该点到四个顶点的距离大于1的概率P=$\frac{{S}_{阴影}}{{S}_{菱形}}$=$1-\frac{{\sqrt{3}π}}{24}$,
故选:A.
点评 本题主要考查几何概型的概率的计算,根据对应分别求出对应区域的面积是解决本题的关键.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:选择题
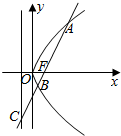 如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )
如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 测试指标 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) |
| 零件数 | 2 | 8 | 32 | 38 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com