
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 求出正四面体的高,进一步得到内切球的半径,由高减去内切球的直径得答案.
解答 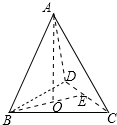 解:设正四面体ABCD的棱长为a,高为h,每一个面的面积为S,其内切球的半径为r,
解:设正四面体ABCD的棱长为a,高为h,每一个面的面积为S,其内切球的半径为r,
则由等积法可得,$\frac{1}{3}Sh=4•\frac{1}{3}Sr$,即$r=\frac{1}{4}h$.
正四面体ABCD的棱长为2,如图,
则BE=$\sqrt{3}$,BO=$\frac{2\sqrt{3}}{3}$,
∴$AO=\sqrt{{2}^{2}-(\frac{2\sqrt{3}}{3})^{2}}=\frac{2\sqrt{6}}{3}$,
∴正四面体内切球的直径为$\frac{\sqrt{6}}{3}$,
则AP的最小值为$\frac{2\sqrt{6}}{3}-\frac{\sqrt{6}}{3}=\frac{\sqrt{6}}{3}$.
故选:A.
点评 本题考查棱锥的结构特征,应熟记正四面体内切球的半径是正四面体高的四分之一这一结论,是中档题.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
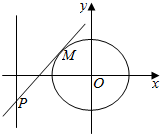 已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
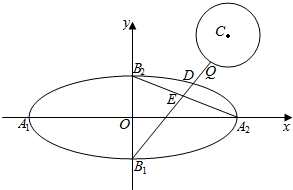 如图,已知椭圆$\frac{{x}^{2}}{2}$+y2=1的四个顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,若圆C:(x-3)2+(y-3)2=r2(0<r<3)上有且只有一个点P满足$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\sqrt{5}$.
如图,已知椭圆$\frac{{x}^{2}}{2}$+y2=1的四个顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,若圆C:(x-3)2+(y-3)2=r2(0<r<3)上有且只有一个点P满足$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com