
分析 将左边分母看作1,然后分子分母同乘以2n+1sinα,将分子逆用正弦的倍角公式化简可得右边.
解答 证明:设sinα≠0,cosα•cos2α•cos22α…cos2nα
=2sinα$\frac{cosα•cos2α•cos{2}^{2}α…cos{2}^{n}α}{2sinα}$
=$\frac{sin2α•cos2α•cos{2}^{2}α…cos{2}^{n}α}{2sinα}$
=$\frac{sin4α•cos{2}^{2}α…cos{2}^{n}α}{{2}^{2}sinα}$
=…
=$\frac{{2}^{\;}sin{2}^{n}αcos{2}^{n}α}{{2}^{n+1}sinα}$
=$\frac{sin{2}^{n+1}α}{{2}^{n+1}sinα}$.
点评 本题考查了三角函数的正弦的倍角公式的逆用;关键是凑出满足公式的形式.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1008 | B. | 2016 | C. | 4032 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
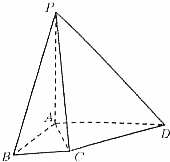 如图,四棱锥P-ABCD中,PA⊥平面ABCD,BC∥AD,∠BAD=120°,AP=AB=AD=2BC.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,BC∥AD,∠BAD=120°,AP=AB=AD=2BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com