
分析 (1)由条件利用二项展开式的通项公式,等差数列的定义,求得n的值,可得展开式的中间项.
(2)在所给的等式中,分别令x=1,x=-1,再把它们相加,可得展开式中含x的奇次幂的系数和.
(3)在所给的等式中,两边分别对x求导数,再令x=1,可得a1+2a2+3a3+…+nan的值.
解答 解:(1)依题意得 ${T_{r+1}}=C_n^r{(-\frac{1}{2})^r}{x^r}$,r=0,1,…,n.
则a0=1,${a_1}=-\frac{n}{2}$,${a_2}={C_n}^2{(-\frac{1}{2})^2}=\frac{n(n-1)}{8}$,
由2|a1|=|a0|+|a2|得n2-9n+8=0可得n=1(舍去),或n=8.
所以${(1-\frac{1}{2}x)^8}$展开式的中间项是${T_5}=C_8^4{(-\frac{1}{2}x)^4}=\frac{35}{8}{x^4}$.
(2)${(1-\frac{1}{2}x)^n}={a_0}+{a_1}x+{a_2}{x^2}+{a_3}{x^3}+…+{a_n}{x^n}$,即${(1-\frac{1}{2}x)^8}={a_0}+{a_1}x+{a_2}{x^2}+{a_3}{x^3}+…+{a_8}{x^8}$,
令x=1得${a_0}+{a_1}+{a_2}+{a_3}+…+{a_8}={(\frac{1}{2})^8}$,令x=-1得${a_0}-{a_1}+{a_2}-{a_3}+…+{a_8}={(\frac{3}{2})^8}$,
两式相减得$2({{a_1}+{a_3}+{a_5}+{a_7}})=\frac{{1-{3^8}}}{2^8}$,即${a_1}+{a_3}+{a_5}+{a_7}=\frac{{1-{3^8}}}{2^9}=-\frac{205}{16}$,
所以展开式中含x的奇次幂的系数和为$-\frac{205}{16}$.
(3)∵${(1-\frac{1}{2}x)^8}={a_0}+{a_1}x+{a_2}{x^2}+{a_3}{x^3}+…+{a_8}{x^8}$,
两边求导得:$-4{(1-\frac{1}{2}x)^7}={a_1}+2{a_2}x+3{a_3}{x^2}+…+8{a_8}{x^7}$,
令x=1得 ${a_1}+2{a_2}+3{a_3}+…+8{a_8}=-4{({\frac{1}{2}})^7}=-\frac{1}{32}$.
点评 本题主要考查等差数列的定义,求函数的导数,二项式定理的应用,二项展开式的通项公式,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于中档题.


科目:高中数学 来源: 题型:选择题
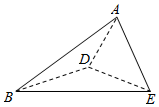 已知三棱锥A-BCD中,△ACD为等边三角形,且平面ACD⊥平面BCD,BD⊥CD,BD=CD=2,则三棱锥A-BCD外接球的表面积为( )
已知三棱锥A-BCD中,△ACD为等边三角形,且平面ACD⊥平面BCD,BD⊥CD,BD=CD=2,则三棱锥A-BCD外接球的表面积为( )| A. | 5π | B. | $\frac{20}{3}$π | C. | 8π | D. | $\frac{28}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b | B. | a<b | C. | a+b=1 | D. | a+b<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com