
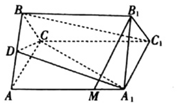
 如图,在正三棱柱ABC-A1B1C1中,点D是AB中点,M是AA1上一点,且AM=tAA1.
如图,在正三棱柱ABC-A1B1C1中,点D是AB中点,M是AA1上一点,且AM=tAA1.分析 (1)取A1B1的中点E,连接BE,C1E.只需证明,面EBC1∥平面A1CD;即可得到BC1∥平面A1CD.
(2)易得CD⊥B1M,要使B1M⊥平面A1CD,只需DA1⊥MB即可,如下图,当DA1⊥MB时,△ADA1∽△A1MB1,⇒$\frac{AD}{{A}_{1}M}=\frac{A{A}_{1}}{{A}_{1}{B}_{1}}$,即可求得t.
解答 解:(1)如图1,取A1B1的中点E,连接BE,C1E.
在正三棱柱ABC-A1B1C1中,点D是AB中点,可得CD∥C1E
又因为DB∥EA1,DB=EA1⇒BE∥DA1.
且CD∩DA1=D,BE∩C1E=E,面EBC1∥平面A1CD;
∵BC1?面EBC1,BC1?平面A1CD,∴BC1∥平面A1CD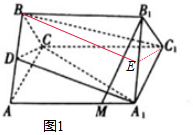
(2)由在正三棱柱ABC-A1B1C1中,点D是AB中点,可得CD⊥面AA1B1B.
⇒CD⊥B1M,
∴要使B1M⊥平面A1CD,只需DA1⊥MB即可,如下图,
当DA1⊥MB时,△ADA1∽△A1MB1,
⇒$\frac{AD}{{A}_{1}M}=\frac{A{A}_{1}}{{A}_{1}{B}_{1}}$,又∵3AB=2AA1,DAB为中点
∴$\frac{\frac{1}{2}AB}{{A}_{1}M}=\frac{A{A}_{1}}{AB}=\frac{3}{2}$⇒${A}_{1}M=\frac{1}{3}AB=\frac{1}{3}×\frac{2}{3}A{A}_{1}=\frac{2}{9}A{A}_{1}$
∴$AM=\frac{7}{9}A{A}_{1}$
即当t=$\frac{7}{9}$时,B1M⊥平面A1CD.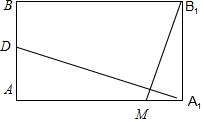
点评 本题考查了空间线面平行的判定,线面垂直的判定,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cosx | B. | $y={x^{\frac{1}{2}}}$ | C. | y=2|x| | D. | y=|lgx| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x(个) | 2 | 3 | 4 | 5 | 6 |
| y(百万元) | 2.5 | 3 | 4 | 4.5 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某超市对某月(30天)每天顾客使用信用卡购物的人数进行了统计,得到如图所示的样本茎叶图,则该样本的中位数、众数、极差分别是( )
某超市对某月(30天)每天顾客使用信用卡购物的人数进行了统计,得到如图所示的样本茎叶图,则该样本的中位数、众数、极差分别是( )| A. | 44,45,56 | B. | 44,43,56 | C. | 44,43,57 | D. | 45,43,57 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com