
| x(个) | 2 | 3 | 4 | 5 | 6 |
| y(百万元) | 2.5 | 3 | 4 | 4.5 | 6 |
分析 (Ⅰ)求出回归系数,可得y关于x的线性回归方程;
(Ⅱ)求出A区平均每个分店的年利润,利用基本不等式,可得结论.
解答 解:(Ⅰ)$\overline{x}$=4,$\overline{y}$=4,$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{\;}({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{8.5}{10}$=0.85,a=$\overline{y}$-$\widehat{b}$$\overline{x}$=4-4×0.85=0.6,
∴y关于x的线性回归方程y=0.85x+0.6.
(Ⅱ)z=y-0.05x2-1.4=-0.05x2+0.85x-0.8,
A区平均每个分店的年利润t=$\frac{z}{x}$=-0.05x-$\frac{0.8}{x}$+0.85=-0.01(5x+$\frac{80}{x}$)+0.85,
∴x=4时,t取得最大值,
故该公司应在A区开设4个分店时,才能使A区平均每个分店的年利润最大
点评 本题考查回归方程,考查基本不等式的运用,正确求出回归方程是关键.


科目:高中数学 来源: 题型:解答题
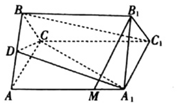 如图,在正三棱柱ABC-A1B1C1中,点D是AB中点,M是AA1上一点,且AM=tAA1.
如图,在正三棱柱ABC-A1B1C1中,点D是AB中点,M是AA1上一点,且AM=tAA1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-2,0) | C. | (0,+∞) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
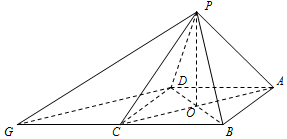 在四棱锥P-ABCD中,底面ABCD为菱形,∠PAD=∠PAB,AC交BD于O,
在四棱锥P-ABCD中,底面ABCD为菱形,∠PAD=∠PAB,AC交BD于O,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com