
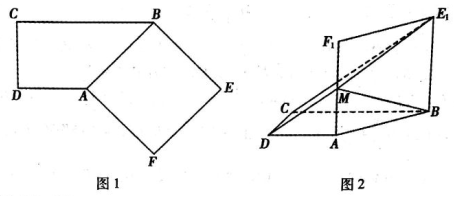
分析 (Ⅰ)只需证明BE1⊥AC.AC⊥AB且AB,可得AC⊥面ABE1F1,AC⊥MB.
(Ⅱ)以B为原点,建立如图所示的空间直角坐标系.
则A(1,1,0),B(0,0,0),C(2,0,0),E1(0,0,$\sqrt{2}$),M(1,1,$\frac{\sqrt{2}}{2}$).利用向量求解
解答 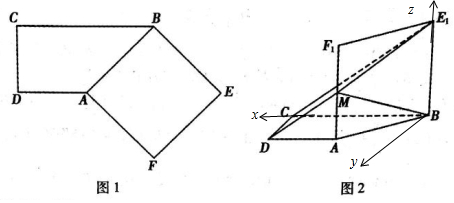 解:(Ⅰ)证明四边形ABE1F1是正方形,∴BE1⊥AB.
解:(Ⅰ)证明四边形ABE1F1是正方形,∴BE1⊥AB.
平面ABE1F1⊥平面ABCD,平面ABE1F1∩平面ABCD=AB,BE1?面ABE1F1
∴BE1⊥平面ABCD,
∵AC?平面ABCD,∴BE1⊥AC.
设AD=1,则AC=AB=$\sqrt{2}$,∴AC⊥AB且AB∩BE1=B.
∴AC⊥面ABE1F1,又MB?面ABE1F1∴AC⊥MB.
(Ⅱ)如图以B为原点,建立如图所示的空间直角坐标系.
则A(1,1,0),B(0,0,0),C(2,0,0),E1(0,0,$\sqrt{2}$),M(1,1,$\frac{\sqrt{2}}{2}$).
由题意得,$\overrightarrow{BM}=(1,1,\frac{\sqrt{2}}{2})$,$\overrightarrow{C{E}_{1}}=(-2,0,\sqrt{2})$,$\overrightarrow{{E}_{1}M}=(1,1,-\frac{\sqrt{2}}{2})$,
设面CE1M的一个法向量为$\overrightarrow{n}=(x,y,z)$,
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{C{E}_{1}}=-2x+\sqrt{2}z=0}\\{\overrightarrow{n}•\overrightarrow{{E}_{1}M}=x+y-\frac{\sqrt{2}}{2}z=0}\end{array}\right.$,可得$\overrightarrow{n}=(1,0,\sqrt{2})$.
又平面ABE1F1得法向量为$\overrightarrow{AC}=(1,-1,0)$.
设平面CE1M与平面ABE1F1所成锐二面角为θ.
cosθ=|cos$<\overrightarrow{AC},\overrightarrow{n}>$|=$\frac{\sqrt{6}}{6}$.
∴平面CE1M与平面ABE1F1所成锐二面角的余弦值为$\frac{\sqrt{6}}{6}$.
点评 本题考查了空间线线垂直的判定,向量法求二面角,转化思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
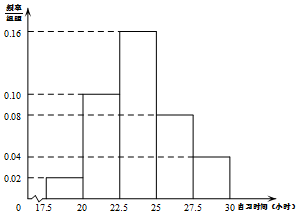 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,若这200名学生中每周的自习时间不超过m小时的人数为164,则m的值约为( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,若这200名学生中每周的自习时间不超过m小时的人数为164,则m的值约为( )| A. | 26.25 | B. | 26.5 | C. | 26.75 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
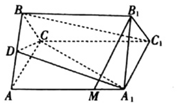 如图,在正三棱柱ABC-A1B1C1中,点D是AB中点,M是AA1上一点,且AM=tAA1.
如图,在正三棱柱ABC-A1B1C1中,点D是AB中点,M是AA1上一点,且AM=tAA1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com