
如图,在直三棱柱ABC?A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,A1A=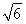 ,M是CC1的中点.
,M是CC1的中点.
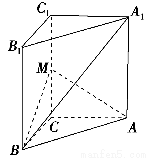
(1)求证:A1B⊥AM;
(2)求二面角B ?AM?C的平面角的大小..
(1)见解析(2)45°
【解析】(1)以点C为原点,CB、CA、CC1所在直线为x,y,z轴,建立空间直角坐标系C-xyz,如图所示,
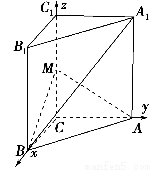
则B(1,0,0),A(0,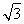 ,0),A1(0,
,0),A1(0,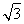 ,
,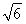 ),M
),M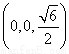 .
.
所以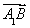 =(1,-
=(1,- ,-
,-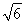 ),
),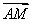 =
= .
.
因为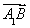 ·
·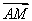 =1×0+(-
=1×0+(-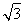 )×(-
)×(-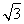 )+(-
)+(-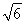 )×
)×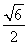 =0,所以A1B⊥AM.
=0,所以A1B⊥AM.
(2)因为ABC ?A1B1C1是直三棱柱,所以CC1⊥平面ABC,又BC?平面ABC,所以CC1⊥BC.
因为∠ACB=90°,即BC⊥AC,又AC∩CC1=C,所以BC⊥平面ACC1A1,即BC⊥平面AMC.
所以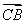 是平面AMC的一个法向量,
是平面AMC的一个法向量,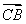 =(1,0,0).
=(1,0,0).
设n=(x,y,z)是平面BAM的一个法向量,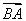 =(-1,
=(-1,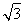 ,0),
,0),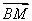 =
= .
.
由 得
得 ,令z=2,得x=
,令z=2,得x=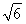 ,y=
,y=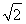 .
.
所以n=(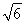 ,
,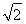 ,2)
,2)
因为|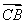 |=1,|n|=2
|=1,|n|=2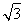 ,所以cos〈
,所以cos〈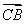 ,n〉=
,n〉=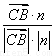 =
=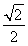 ,
,
因此二面角B ?AM?C的大小为45°


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练倒数第8天练习卷(解析版) 题型:填空题
已知l,m是两条不同的直线,α,β是两个不同的平面,下列命题:
①若l?α,m?α,l∥β,m∥β,则α∥β;
②若l?α,l∥β,α∩β=m,则l∥m;
③若α∥β,l∥α则l∥β;
④若l⊥α,m∥l,α∥β,则m⊥β.
其中真命题是______________(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练倒数第5天练习卷(解析版) 题型:填空题
若圆x2+y2=4与圆x2+y2+2ay-6=0(a>0)的公共弦的长为2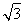 ,则a=________.
,则a=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练倒数第3天练习卷(解析版) 题型:解答题
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证:
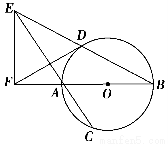
(1)∠AED=∠AFD;
(2)AB2=BE·BD-AE·AC.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练倒数第10天练习卷(解析版) 题型:填空题
设A是整数集的一个非空子集,对于k∈A,如果k-1∉A且k+1∉A,那么k是A的一个“孤立元”,给定S={1,2,3,4,5,6,7,8},由S的3个元素构成的所有集合中,不含“孤立元”的集合共有________个.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练倒数第10天练习卷(解析版) 题型:填空题
已知集合A={x|x>5},集合B={x|x>a},若命题“x∈A”是命题“x∈B”的充分不必要条件,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第四章第4课时练习卷(解析版) 题型:解答题
已知m∈R,复数z=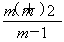 +(m2+2m-3)i,当m为何值时.
+(m2+2m-3)i,当m为何值时.
(1)z∈R;(2)z是虚数;(3)z是纯虚数.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第四章第2课时练习卷(解析版) 题型:填空题
已知四边形ABCD的三个顶点A(0,2),B(-1,-2),C(3,1),且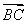 =2
=2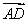 ,则顶点D的坐标为________.
,则顶点D的坐标为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com