
| A. | y2=x | B. | y2=2x | C. | y2=4x | D. | y2=8x |
分析 分别过A、B作准线的垂线,利用抛物线定义将A、B到焦点的距离转化为到准线的距离,利用△BCD∽△FCG即可得p值,进而可得方程.
解答 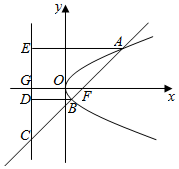 解:分别过点A,B作准线的垂线,分别交准线于点E,D
解:分别过点A,B作准线的垂线,分别交准线于点E,D
由$\overrightarrow{CB}$=2$\overrightarrow{BF}$,可知:丨$\overrightarrow{CB}$丨=2丨$\overrightarrow{BF}$丨,设|BF|=a,则|BC|=2a,|BD|=a,
∴∠BCD=30°,
在直角三角形ACE中,
∵|AF|=2,|AC|=2+3a,
∴2|AE|=|AC|,
∴2+3a=4,即a=$\frac{2}{3}$,
|CF|=2,
∴sin∠BCD=$\frac{丨GF丨}{丨CF丨}$=$\frac{p}{2}$,解得p=1,
∴抛物线方程为y2=2x.
故选:B.
点评 本题考查抛物线的定义及其应用,抛物线的几何性质,过焦点的弦的弦长关系,转化化归的思想方法,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | y2=8x | B. | y2=-8x | C. | y2=4x | D. | y2=-4x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $-\frac{2}{3}$ | C. | $-\frac{{2\sqrt{2}}}{3}$ | D. | $-\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | $3\sqrt{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{3\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
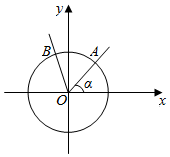 如图,锐角α的顶点在坐标原点,始边与x轴正半轴重合,终边与单位圆交于点A(x1,y1),将射线OA绕原点按逆时针方向旋转$\frac{π}{3}$后与单位圆交于点B(x2,y2),记函数f(α)=y1+y2.
如图,锐角α的顶点在坐标原点,始边与x轴正半轴重合,终边与单位圆交于点A(x1,y1),将射线OA绕原点按逆时针方向旋转$\frac{π}{3}$后与单位圆交于点B(x2,y2),记函数f(α)=y1+y2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com