
| �������� | ����� |
| [0��60�� | 100 |
| [60��85�� | 200 |
| [85��100] | 300 |
| �ܼ� | 600 |
���� �����ݳ������飬���������[0��60���ĸ��ʣ��Ӷ�������ֲ�����60�ֵĸ��ʼ��ɣ��������������ʵĹ�ʽ���㼴�ɣ�
��� �⣺����������ã�
������[0��60���ĸ���p=$\frac{1}{6}$��
��[60��85���ĸ���p=$\frac{1}{3}$��
��[85��100���ĸ�����p=$\frac{1}{2}$��
��6���и��ο͵����ֲ�����60�ֵĸ�����1-$\frac{1}{6}$=$\frac{5}{6}$��
������������6���ο��У�
���ѡȡ�����οͽ�����̸��
���������ο͵�����ȫΪ���������ĸ���p=$\frac{{C}_{3}^{2}}{{C}_{6}^{2}}$=$\frac{1}{5}$��
���� ���⿼���˳������飬�����������ʣ���һ�������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\frac{5}{2}$ | C�� | -2 | D�� | -$\frac{5}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 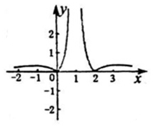 | B�� | 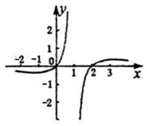 | ||
| C�� | 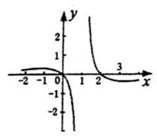 | D�� | 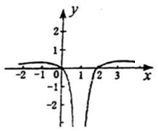 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1��3} | B�� | {0��2} | C�� | {1} | D�� | {-1��1��3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com